
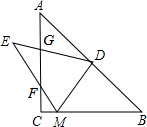
 如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.
如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.分析 (1)等腰直角三角形的性质可知∠B=45°,由三角形的内角和定理可知;∠BDM+∠BND=135°,由翻折的性质可知;∠EDB+∠EMB=270°,由邻补角的定义可求得:∠ADE+∠EMC=360°-(∠EDB+∠EMB);
(2)首先由等腰直角三角形的性质可知∠A=∠B=45°,然后根据直角三角形斜边上的中线的性质可知:CD=BD=AD,∠ACD=45°,然后由折叠的性质可知:DB=DE,∠DEM=45°,从而可证明∠FEC=∠FCE.于是可得到EF=FC,然后结合折叠的性质可证明BC=12.
解答 解:(1)∵△ABC为等腰直角三角形,
∴∠B=45°.
在△BMD中,∠BDM+∠BND=180°-∠B=135°,
由翻折的性质可知:∠EDM=BDM,∠EMD=∠BMD,
∴∠EDB+∠EMB=270°,
∵∠ADE=180°-∠EDB,∠EMC=180°-∠EMB,
∴∠ADE+∠EMC=360°-(∠EDB+∠EMB)=360°-270°=90°.
(2)如图,连接CD、DF、CE.
∵点D为AB的中点,∠C=90°,
∴CD=$\frac{1}{2}$AB,BD=$\frac{1}{2}$AB,
∴CD=BD
由折叠的性质可知:BD=DE,
∴CD=ED.
∴∠DCE=∠DEC.
∵△ACB为等腰直角三角形,
∴∠ABC=45°
∵CD=DB,
∴∠DCB=45°.
∴∠ACM=45°
由折叠的性质可知:∠DEM=∠DBM=45°,EM=BM,
∴∠FEC=∠FCE.
∴EF=FC.
△FCM的周长=FC+FM+CM=FE+FM+CM=EM+CM=MB+CM=CB,
∴BC=12.
点评 本题主要考查的是折叠的性质、等腰直角三角形的性质,直角三角形斜边上中线的性质以及勾股定理的应用,证得三角形FCM的周长等于BC是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么正确的平移方法是向右平移2个格,再向下平移3个格.
如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么正确的平移方法是向右平移2个格,再向下平移3个格.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com