
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理得到AF=![]() =
=![]() =
=![]() ,根据平行线分线段成比例定理得到,OH=
,根据平行线分线段成比例定理得到,OH=![]() AE=
AE=![]() ,由相似三角形的性质得到
,由相似三角形的性质得到![]() =
=![]() ,求得AM=
,求得AM=![]() AF=
AF=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() =
=![]() ,求得AN=
,求得AN=![]() AF=
AF=![]() ,即可得到结论.
,即可得到结论.
过F作FH⊥AD于H,交ED于O,则FH=AB=2.
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF=![]() =
=![]() =
=![]() ,
,
∵OH∥AE,
∴![]() =
=![]() ,
,
∴OH=![]() AE=
AE=![]() ,
,
∴OF=FH﹣OH=2﹣![]() =
=![]() ,
,
∵AE∥FO,∴△AME∽△FMO,
∴![]() =
=![]() ,∴AM=
,∴AM=![]() AF=
AF=![]() ,
,
∵AD∥BF,∴△AND∽△FNB,
∴![]() =
=![]() ,
,
∴AN=![]() AF=
AF=![]() ,
,
∴MN=AN﹣AM=![]() ﹣
﹣![]() =
=![]() ,故选B.
,故选B.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (-3,-1) D. (-3,
) C. (-3,-1) D. (-3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)求三辆车全部同向而行的概率;
(2)求至少有两辆车向左转的概率;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,它是把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,将这种做法继续下去(如图2,图3…).观察规律解答以下各题:
 ……
……
(1)填写下表:
图形序号 | 挖去三角形的个数 |
图1 | 1 |
图2 | 1+3 |
图3 | 1+3+9 |
图4 |
(2)根据这个规律,求图n中挖去三角形的个数fn(用含n的代数式表示);
(3)若图n+1中挖去三角形的个数为fn+1,求fn+1-fn
查看答案和解析>>
科目:初中数学 来源: 题型:
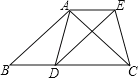
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
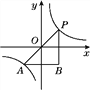
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了准备“迎新活动”,用700元购买了甲、乙两种小礼品260个,其中购买甲种礼品比乙种礼品少用了100元.
(1)购买乙种礼品花了______元;
(2)如果甲种礼品的单价比乙种礼品的单价高20%,求乙种礼品的单价.(列分式方程解应用题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C,请问AB与MN平行吗?说明理由.完成下列推理过程:

解:AB∥MN.理由如下:
∵EF⊥AC,DB⊥AC,(已知),
∴∠CFE=∠CMD=90°,( )
∴EF∥DM,( )
∴∠2=∠CDM,( )
∵∠1=∠2,(已知),
∴∠1=∠ ( )
∴MN∥CD,( )
∵∠3=∠C,(已知),
∴AB∥CD,( ),
∴AB∥MN.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划在春节期间组织员工![]() 人去旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元人.两家旅行社对10人以上的团体推出了不同的优惠措施:甲旅行社对每位员工七五折优惠:乙旅行社免去一位带队员工的费用,其余员工八折优惠
人去旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元人.两家旅行社对10人以上的团体推出了不同的优惠措施:甲旅行社对每位员工七五折优惠:乙旅行社免去一位带队员工的费用,其余员工八折优惠
(1)求甲、乙两家旅行社的费用分别为多少元?(用含 ![]() 的代数式表示)
的代数式表示)
(2)若该单位组织包括带队员工在内共20名员工去旅游,你认为该单位选择哪家旅行社比较优惠?并通过计算说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com