
����Ŀ������֪����y=x��ͼ������ƽ��1����λ�õ�y=x��1��ͼ�����Ƶģ�y=![]() ��k��0����ͼ������ƽ��2����λ�õ�y=
��k��0����ͼ������ƽ��2����λ�õ�y=![]() ��k��0����ͼ����������һ֪ʶ������⣮
��k��0����ͼ����������һ֪ʶ������⣮
��ͼ����֪����������y=![]() ��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��1��m���͵�B��
��ͼ��C������������y=ax��a��0����ͼ��l�ཻ�ڵ�A��1��m���͵�B��
��1��д����B�����꣬����a��ֵ��
��2��������y=![]() ��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC1��l1����֪ͼ��C1������M��3��2����
��ͼ���ֱ��ABͬʱ����ƽ��n��n��0������λ���ȣ��õ���ͼ��ֱ��ΪC1��l1����֪ͼ��C1������M��3��2����
�ٷֱ�д��ƽ�ƺ������ͼ��C1��l1��Ӧ�ĺ�����ϵʽ��
��ֱ��д������ʽ![]() +4��ax�Ľ⼯��
+4��ax�Ľ⼯��
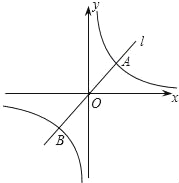
���𰸡���1��a=2��B������Ϊ����1����2������2����C���Ľ���ʽΪy=![]() ��ͼ��l���Ľ���ʽΪy=2x��4����1��x��2��x��3��
��ͼ��l���Ľ���ʽΪy=2x��4����1��x��2��x��3��
�������������������1��ֱ�Ӱ�A���������y=![]() �������m��ֵ��Ȼ���ٰ�A����������y=ax�����a��ֵ�����÷�����������ͼ����������������ͼ��Ľ������ԭ��Գ�ȷ��B�����ꣻ
�������m��ֵ��Ȼ���ٰ�A����������y=ax�����a��ֵ�����÷�����������ͼ����������������ͼ��Ľ������ԭ��Գ�ȷ��B�����ꣻ
��2����������õ�����y=![]() ��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪy=
��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C��Ľ���ʽΪy=![]() ��Ȼ���M��������뼴�ɵõ�n��ֵ��
��Ȼ���M��������뼴�ɵõ�n��ֵ��
�ٸ���������ͼ��C��Ľ���ʽΪy=![]() ��ͼ��l1�Ľ���ʽΪy=2x-4��
��ͼ��l1�Ľ���ʽΪy=2x-4��
�ڲ���ʽ![]() +4��ax������Ϊ�Ƚ�y=
+4��ax������Ϊ�Ƚ�y=![]() ��y=2x-4�ĺ���ֵ������y=
��y=2x-4�ĺ���ֵ������y=![]() ��y=2x-4Ϊ����y=
��y=2x-4Ϊ����y=![]() ��ͼ���ֱ��ABͬʱ����ƽ��2����λ���ȣ��õ���ͼ�ⲻ��ʽ
��ͼ���ֱ��ABͬʱ����ƽ��2����λ���ȣ��õ���ͼ�ⲻ��ʽ![]() ��2x4�ó��⼯��
��2x4�ó��⼯��
�����������1����A��1��m������y=![]() �ã�m=
�ã�m=![]() =2
=2
�ѵ�A��1��2������y=ax��a=2
�߷���������y=![]() ��ͼ��������������y=2x��ͼ��Ľ������ԭ��Գƣ�
��ͼ��������������y=2x��ͼ��Ľ������ԭ��Գƣ�
��B����������1����2����
��2������y=![]() ��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C���Ľ���ʽΪy=
��ͼ������ƽ��n��n��0������λ���ȣ��õ���ͼ��C���Ľ���ʽΪy=![]() ��
��
��M��3��2������2=![]() ����n=2��
����n=2��
�ٸ���������ͼ��C���Ľ���ʽΪy=![]() ��ͼ��l���Ľ���ʽΪy=2��x��2��=2x��4��
��ͼ��l���Ľ���ʽΪy=2��x��2��=2x��4��
��ƽ���Ժ���������ͼ��Ľ���ֱ��ǣ�1����2������3��2�������Բ���ʽΪ![]() �����ͼ��֪�⼯Ϊ1��x��2��x��3��
�����ͼ��֪�⼯Ϊ1��x��2��x��3��



 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У���ABC��90�㣬AB��BC�������εĶ������ƽ�е�����ֱ��l1��l2��l3�ϣ���l1��l2֮��ľ���Ϊ2��l2��l3֮��ľ���Ϊ3����AC�ij���_________��
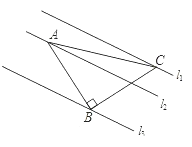
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж���һ�ֹ���n�����㣺�ٵ�n������ʱ�����Ϊ3n+5�ڵ�nΪż��ʱ�������![]() ������k��ʹ
������k��ʹ![]() �����������������������ظ����У��磺ȡn��26����26
�����������������������ظ����У��磺ȡn��26����26![]() 13
13![]() 44
44![]() 11������n��449�����449������Ľ���ǣ�������
11������n��449�����449������Ľ���ǣ�������
A.1B.2C.7D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ཻ��
��ֱ��ཻ��![]() .��
.��![]() ������Ϊ
������Ϊ![]() ����
����![]() ���߶�
���߶�![]() �ϵ�һ��.
�ϵ�һ��.

��1����![]() ��ֵ����2����
��ֵ����2����![]() �����Ϊ2�����
�����Ϊ2�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��������P��2��2�����ֱ�x�ᡢy���ڵ�A��4��0����B��
��1����ֱ��l1�Ľ���ʽ��
��2����CΪx�Ḻ������һ�㣬����C��ֱ��l2��![]() ���߶�AB�ڵ�D��
���߶�AB�ڵ�D��
��ͼ1������Dǡ���P�غ�ʱ����Q��t��0��Ϊx����һ���㣬����Q��QM��x�ᣬ�ֱ�ֱ��l1��l2�ڵ�M��N����![]() ��MN=2MQ����t��ֵ��
��MN=2MQ����t��ֵ��
��ͼ2����BC=CD�����ж�m��n֮���������ϵ��˵�����ɡ�
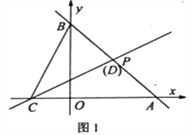

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺��ͼ1����![]() ��ֱ��
��ֱ��![]() ������.������
������.������![]() ���ת����ֱ��
���ת����ֱ��![]() ֮��ľ���ʼ�ձ��ֲ��䣨������
֮��ľ���ʼ�ձ��ֲ��䣨������![]() �İ뾶��.���ǰѾ�����һ���Ե�ͼ�γ�Ϊ���ȿ�������.ͼ2������Բ����һ���Ե�����.����ֱ����Բ�������������棬ͨ��Բ���������ý�С�����Ϳ����ƶ�����ǰ��.��˵���Ű�����������ֻ�еķ�������ʯ�Ƶ�����������.
�İ뾶��.���ǰѾ�����һ���Ե�ͼ�γ�Ϊ���ȿ�������.ͼ2������Բ����һ���Ե�����.����ֱ����Բ�������������棬ͨ��Բ���������ý�С�����Ϳ����ƶ�����ǰ��.��˵���Ű�����������ֻ�еķ�������ʯ�Ƶ�����������.

��չӦ�ã���ͼ3��ʾ�Ļ������Σ�Ҳ��Ϊ���������Σ�Ҳ�����ȿ�������.��ͼ4������ƽ����![]() ֮�������������������ô������ƽ����ľ���ʼ�ղ���.��ֱ��
֮�������������������ô������ƽ����ľ���ʼ�ղ���.��ֱ��![]() ֮��ľ������
֮��ľ������![]() �������������ε��ܳ�Ϊ
�������������ε��ܳ�Ϊ ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ��:
С��ͬѧ��ѧϰ��������������һ��������������4��2.112��4��2.11��2.22��2.222����������̫�鷳������Ӧ���п��Լ���ķ�������ȥ��̴���ʦ������ʦ˵:���������������Ϳ���֪������μ�����!
��ȡ��֪:
�����С��һ����ɴ���ʦ�ṩ������:
��1������:
x����1��y��1 | x��1��y��0 | x��3��y��2 | x��2��y����1 | x��2��y��3 | |
A��2x��y | ��3 | 2 | 4 | 5 | 1 |
B��4x2��4xy��y2 | 9 | 4 | 16 |
��2���۲�����㷢��A��B��ʲô��ϵ?
�������:
��3��������A��B֮��Ĺ�ϵ����:4��2.112��4��2.11��2.22��2.222��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�����ʽ����ѧϰ��,����ͨ����ͬһ����IJ�ͬ����ͱȽ�,�õ��ϲ�ͬ����ķ������������������ַ������о����㡣
��1��������⣺47��43��56��54��89��81��������һЩʮλ����ͬ���Ҹ�λ��֮����10��������λ����˵���ʽ���Ƿ�����ҵ�һ�����㷽����
��2�����ν�ģ��
�ó����ε������ʾ���������ij˻�����47��43Ϊ����
(1)����Ϊ47����Ϊ43�ľ��Σ���ͼ�������47��43�ľ��δ��ұ����³�40����3��һ����ƴ�ӵ�ԭ����������.

(2)ԭ������������������ֲ�ͬ�ı��﷽ʽ��47��43�ľ��������(40+7+3)��40�ľ��������Ͻ�3��7�ij��������֮��,��47��43=(40+10)��40+3��7=5��4��100+3��7=2021��
��3��ģ��Ӧ��:
�����������ķ���ʹ�ó����ε������ʾ56��54�ij˻���
����գ�89��81= ��8��100�� �� =7209;
(4)��������:
����ʮλ������ͬ,���Ҹ�λ����֮����10����λ����˵����㷽����(�����ֱ���) .
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com