
【题目】如图,在△ABC中,AB=AC,D在边AC上,且BD=DA=BC.
(1)如图1,填空:∠A=_______.
(2)如图2,若M为线段AC上的点,过M作直线MH⊥BD于H,分别交直线AB、BC于点N、E.
①求证:△BNE是等腰三角形;
②试写出线段AN、CE、CD之间的数量关系,并说明理由.

【答案】(1)36°;(2)①证明见解析;②AN+CE=CD,理由见解析.
【解析】
(1)根据等腰三角形的性质得到∠A=∠DBA=∠DBC=![]() ∠ABC=
∠ABC=![]() ∠C,根据三角形的内角和即可得到结论;
∠C,根据三角形的内角和即可得到结论;
(2)①根据已知条件得到∠ABD=∠CBD=36°,根据垂直的定义得到∠BHN=∠EHB=90°,根据全等三角形的性质即可得到结论;
②由①知,BN=BE,根据线段的和差和等量代换即可得到结论.
解:(1)∵BD=BC,
∴∠BDC=∠C,
∵AB=AC,
∴∠ABC=∠C,
∴∠A=∠DBC,
∵AD=BD,
∴∠A=∠DBA,
∴∠A=∠DBA=∠DBC=![]() ∠ABC=
∠ABC=![]() ∠C,
∠C,
∵∠A+∠ABC+∠C=5∠A=180°,
∴∠A=36°,∠C=72°;
故答案为:36°;
(2)①∵BD=AD,
∴∠A=∠ABD
∵∠BDC=∠A+∠ABD,
∴∠BDC=2∠ABD
∵BD=BC,
∴∠BCD=2∠ABD
∵AB=AC,
∴∠ABC=∠ACB=2∠ABD,
∴∠ABD=∠CBD
∵MH⊥BD于H,
∴NHBEHB
在△NBH与△EBH中
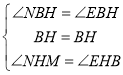
∴△NHB≌△EBH(ASA),
∴BN=BE,
∴△BNE为等腰三角形;

②AN+CE=CD
∵AB=AC
∴AN+BN=AD+DC
∵BN=BE,
∴AN+BE=AD+DC,
∴AN+BC+CE=AD+DC
∵BC=AD,
∴AN+CE=CD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE中.
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
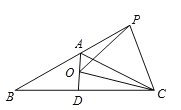
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:
①∠APO+∠DCO=30°;②△OPC是等边三角形:③AC=DO+AP;④S△ABC=S四形形AOCP.
其中正确的是_______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(Ⅰ)如图①,若⊙O的半径为5,求线段OC的长;
(Ⅱ)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
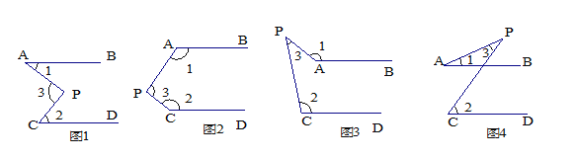
如下面四个图形中, AB∥CD.
(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.
(2)请你从中任选一个加以说明理由.
解决问题:
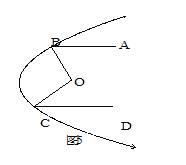
(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)求证:∠AEB=∠ACF;
(2)求证:EF2BF22AC2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com