
【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
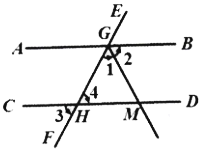
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.( )
∵∠3=60°,(已知)
∴∠4=60°.( )
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.( )
∴∠FGB= .
∵GM平分∠FGB,(已知)
∴∠1= °.(角平分线的定义)
 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某林场计划购买甲、乙两种树苗共1000株,甲种树苗每株12元,乙种树苗每株15元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去13200元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE是平行四边形ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E,连接AC,BE,则下列结论:①AC=AD;②AO=![]() ;③四边形ACBE是菱形;④
;③四边形ACBE是菱形;④![]() .其中正确的结论有____.(填写所有正确结论的序号)
.其中正确的结论有____.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)参与问卷调查的总人数为 ,扇形统计图中“B”对应的扇形的圆心角度数等于 °;
(2)补全条形统计图.
(3)该社区中20~60岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格如下表所示:

某中学七年级(1)、(2)两个班计划去游览该公园,其中(I)班的人数较少,不足 50 人;(2) 班人数略多,有 50 多人.如果两个班都以班为单位分别购票,则一共应付 1172 元,如 果两个班联合起来,作为一个团体购票,则需付 1078 元.
(1)列方程求出两个班各有多少学生;
(2)如果两个班联合起来买票,是否可以买单价为 9 元的票?你有什么省钱的方法来帮 他们买票呢?请给出最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
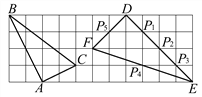
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com