
 如图,AC,BD为⊙O的两条弦,AC,BD相交于点P,
如图,AC,BD为⊙O的两条弦,AC,BD相交于点P,分析 (1)连接BC,如图1,①根据圆心角、弧、弦的关系由AC=BD得到$\widehat{AC}$=$\widehat{BD}$,然后利用等量减等量差相等即可得到$\widehat{AB}$=$\widehat{CD}$;②根据圆周角定理由$\widehat{AB}$=$\widehat{CD}$得到∠C=∠B,然后根据等腰三角形的判定定理可得BP=CP;
(2)作OM⊥AC于M,ON⊥BD于N,如图2,根据角平分线定理得OM=ON,然后根据圆心角、弧、弦的关系得到AC=BD,再与(1)一样可得BP=CP.
解答  证明:(1)连接BC,如图1,
证明:(1)连接BC,如图1,
①∵AC=BD,
∴$\widehat{AC}$=$\widehat{BD}$,
∴$\widehat{AC}$-$\widehat{AD}$=$\widehat{BD}$-$\widehat{AD}$,
∴$\widehat{AB}$=$\widehat{CD}$;
②∵$\widehat{AB}$=$\widehat{CD}$,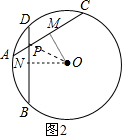 ∴∠C=∠B,
∴∠C=∠B,
∴BP=CP;
(2)作OM⊥AC于M,ON⊥BD于N,如图2,
∵OP平分∠BPC,
∴OM=ON,
∴AC=BD,
由(1)得BP=CP.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了圆周角定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
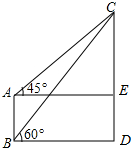 如图:从B处测得建筑物上旗杆EC顶点C的仰角是60°,再从B的正上方40米高层上A处,测得C的仰角是45°,那么旗杆顶点C离地CD的高度是( )米.
如图:从B处测得建筑物上旗杆EC顶点C的仰角是60°,再从B的正上方40米高层上A处,测得C的仰角是45°,那么旗杆顶点C离地CD的高度是( )米.| A. | 18$\sqrt{3}$+40 | B. | 19$\sqrt{3}$+50 | C. | 20$\sqrt{3}$+60 | D. | 21$\sqrt{3}$+70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | π、R是变量,2为常量 | B. | C、R为变量,2、π为常量 | ||
| C. | R为变量,2、π、C为常量 | D. | C为变量,2、π、R为常量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com