

分析 (1)直接利用切线的性质得出OC⊥PC,OD⊥PD,进而利用四边形内角和定理得出答案;
(2)利用圆周角定理结合三角形的外角的性质得出答案;
(3)首选利用正方形的判定与性质得出∠PCO=∠COD=90°,进而得出△COK≌△ODF(AAS),再利用勾股定理以及平行线的性质得出OG的长.
解答 (1)证明:∵PC、PD分别切⊙O于点C、D,
∴OC⊥PC,OD⊥PD,
∴∠PCO=∠PDO90°,
∴∠P+∠COD=360°-90°-90°=180°;
(2)证明:∵∠B=$\frac{1}{2}$∠AOC,∠A=$\frac{1}{2}$∠BOD,
∴∠AEC=∠A+∠B=$\frac{1}{2}∠AOC+\frac{1}{2}∠BOD$,
=$\frac{1}{2}$(∠AOC+∠BOD),
=$\frac{1}{2}$(180°-∠COD),
=$\frac{1}{2}$∠P;
(3)解:∵PC、PD分别切⊙O于点C、D,
∴PC=PD,
∵PC+PD=2AB,
∴CO=DO=AO=CO=DO,
∴四边形PCOD是菱形,
∴∠P=∠COD,OD∥PH,
∴∠P=∠COD=90°,
∴四边形PCOD是正方形,
∴∠PCO=∠COD=90°,
如图3,过O作OK⊥AD交PC于点,
∴∠HKO+∠COK=90°,∠DFO+∠COK=90°,
∴∠HKO=∠DFO,
在△COK和△ODF中
$\left\{\begin{array}{l}{∠OKC=∠DFO}\\{∠KCO=∠OD}\\{CO=DO}\end{array}\right.$,
∴△COK≌△ODF(AAS),
∴CK=OF=4,
∵∠DFO+∠ODF=90°,
∴∠COK=∠ODF+∠OAD,
∵∠DFO=∠OAD+∠AOC=∠COK+∠AOC=∠AOK,
∴AK=AO,
设CF=x,则CH=2x,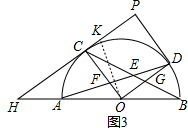
∴HO=HK=2x+4,
在Rt△OCH中,(x+4)2+(2x)2=(2x+4)2,
解得:x=0或x=8,
∴CH=16,BO=OC=4+8=12,HO=HK=20,
∵DO∥HP,
∴$\frac{BO}{HB}$=$\frac{OG}{CH}$,
即:$\frac{12}{32}$=$\frac{GO}{16}$,
∴OG=6.
点评 此题主要考查了圆的综合以及全等三角形的判定与性质和正方形的判定与性质等知识,正确得出FC的长是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
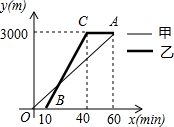 甲、乙两人从学校沿同一路线到距学校3000m的图书馆看书,甲先出发,他们距学校的路程y(m)与甲的行走时间x(min)之间的函数图象如图所示,根据图象解答下列问题:
甲、乙两人从学校沿同一路线到距学校3000m的图书馆看书,甲先出发,他们距学校的路程y(m)与甲的行走时间x(min)之间的函数图象如图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com