
分析 将已知变形可得a2+a=1,将所求分式整理为含a2+a的式子,然后代入a2+a=1即可得出结论.
解答 解:∵a2=$(\frac{\sqrt{5}-1}{2})^{2}$=$\frac{3-\sqrt{5}}{2}$=1-a,
∴a2+a=1.
∴$\frac{{a}^{5}+{a}^{4}-2{a}^{3}-{a}^{2}-a+2}{{a}^{3}-a}$=$\frac{{a}^{3}({a}^{2}+a)-2{a}^{3}-({a}^{2}+a)+2}{a(a+1)(a-1)}$=$\frac{1-{a}^{3}}{a-1}$=-(1+a+a2)=-2.
点评 本题主要考查分式的化简求值问题,将所求分式整理为含a2+a的结构形式并整体代入是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
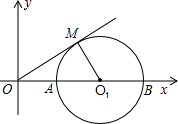 如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:
某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔,每位女生的身高(cm)统计如图,部分统计量如表:| 平均数 | 标准差 | 中位数 | |
| 甲队 | 1.72 | 0.038 | 1.73 |
| 乙队 | 1.69 | 0.025 | 1.70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,分别以AD、BC为边作Rt△ADE和Rt△BFC,延长DE、FB交于点P,延长FC、AE交于点Q,连接AP、QB,延长QB交PD于点N,交AP于点M,若PD=$\sqrt{5}$AM,PM=2BN,则tan∠DAQ的值为$\frac{8\sqrt{5}}{15}$.
如图,在正方形ABCD中,分别以AD、BC为边作Rt△ADE和Rt△BFC,延长DE、FB交于点P,延长FC、AE交于点Q,连接AP、QB,延长QB交PD于点N,交AP于点M,若PD=$\sqrt{5}$AM,PM=2BN,则tan∠DAQ的值为$\frac{8\sqrt{5}}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个3×3的网格(每个小正方形的边长为1,三个顶点都在小正方形的顶点上的三角形叫作格点三角形).
如图是一个3×3的网格(每个小正方形的边长为1,三个顶点都在小正方形的顶点上的三角形叫作格点三角形).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com