
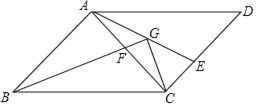
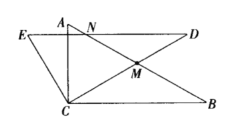
【题目】在平行四边形ABCD中,∠ABC=45°,AB=AC,点E,F分别CD、AC边上的点,且AF=CE,BF的延长线交AE于点G.
(1)若DE=2![]() ,AD=8,求AE.
,AD=8,求AE.
(2)若G是AE的中点,连接CG,求证:![]() AE+CG=BG.
AE+CG=BG.
【答案】(1)2![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)证明△ABC是等腰直角三角形,得出CD=AB=AC=![]() BC=4
BC=4![]() ,求出CE=CD-DE=2
,求出CE=CD-DE=2![]() ,由勾股定理即可得出答案;
,由勾股定理即可得出答案;
(2)证明△ABF≌△CAE(SAS),得出BF=AE,∠ABF=∠CAE,取BF的中点H,连接AH,由直角三角形斜边上的中线性质得出AH=![]() BF=BH,CG=
BF=BH,CG=![]() AE=AG,得出∠ABF=∠BAH,证出∠BAH=∠CAE,证出∠GAH=∠BAF=90°,得出AH=AG=BH=CG,因此△GAH是等腰直角三角形,得出GH=
AE=AG,得出∠ABF=∠BAH,证出∠BAH=∠CAE,证出∠GAH=∠BAF=90°,得出AH=AG=BH=CG,因此△GAH是等腰直角三角形,得出GH=![]() AG=
AG=![]() AE,即可得出结论.
AE,即可得出结论.
(1)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=8,
∵∠ABC=45°,AB=AC,
∴∠ACB=∠ABC=45°,
∴ACD=∠BAC=90°,
∴△ABC是等腰直角三角形,
∴CD=AB=AC=![]() BC=4
BC=4![]() ,
,
∵DE=2![]() ,
,
∴CE=CD﹣DE=2![]() ,
,
∴AE=![]() =
=![]() =2
=2![]() ;
;
(2)证明:在△ABF和△CAE中,
 ,
,
∴△ABF≌△CAE(SAS),
∴BF=AE,∠ABF=∠CAE,
取BF的中点H,连接AH,如图所示:
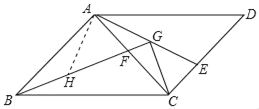
∵∠BAF=90°,AH=![]() BF=BH,
BF=BH,
∴∠ABF=∠BAH,
∴∠BAH=∠CAE,
∴∠GAH=∠BAF=90°,
∵∠ACF=90°,G是AE的中点,
∴CG=![]() AE=AG,
AE=AG,
∴AH=AG=BH=CG,
∴△GAH是等腰直角三角形,
∴GH=![]() AG=
AG=![]() AE,
AE,
∴![]() AE+CG=GH+BH=BG.
AE+CG=GH+BH=BG.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购买50根跳绳,如果A型跳绳的数量不多于B型跳绳数量的3倍,那么A型跳绳最多能买多少条?
查看答案和解析>>
科目:初中数学 来源: 题型:
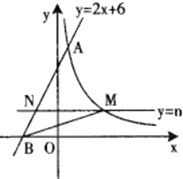
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 与
与![]() 轴交于点
轴交于点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 交反比例函数的图象于点
交反比例函数的图象于点![]() 交线段
交线段![]() 于点
于点![]() 连接
连接![]() .
.
(1)求![]() 的值和反比例函数的表达式;
的值和反比例函数的表达式;
(2)当点![]() 是线段
是线段![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
(3)直线![]() 沿
沿![]() 轴方向平移,当
轴方向平移,当![]() 为何值时,
为何值时,![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,![]() 交直线
交直线![]() 于
于![]() .发现:
.发现:![]() .
.
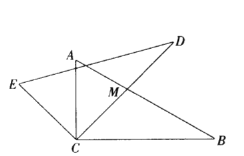
探究①:若![]() 恰好是
恰好是![]() 的中点,
的中点,![]() 交
交![]() 于
于![]() ,如图2,求
,如图2,求![]() 的长;
的长;
探究②:在旋转过程中,当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 所旋转的路径长(保留
所旋转的路径长(保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜坡AB长10米,按图中的直角坐标系可用![]() 表示,点A,B分别在x轴和y轴上,且
表示,点A,B分别在x轴和y轴上,且![]() .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用
.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用![]() 表示.
表示.
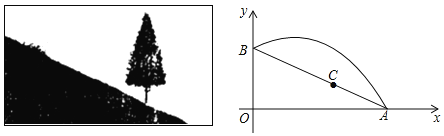
(1)求抛物线的函数关系式(不必写自变量取值范围);
(2)求水柱离坡面AB的最大高度;
(3)在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数 | 22 | 52 | 68 | 101 | 116 | 147 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.45 | 0.51 | 0.46 | 0.49 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是__________(填写序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com