
分析 (1)根据平方差公式与多项式乘以多项式的运算法则运算即可;
(2)根据(1)的规律可得结果;
(3)原式变形后,利用(2)得出的规律计算即可得到结果.
解答 解:(1)(a-b)(a+b)=a2-b2;
(a-b)(a2+ab+b2)=a3+a2b+ab2-a2b-ab2-b3=a3-b3;
(a-b)(a3+a2b+ab2+b3)=a4+a3b+a2b2+ab3-a3b-a2b2-ab3-b4=a4-b4;
故答案为:a2-b2,a3-b3,a4-b4;
(2)由(1)的规律可得:原式=an-bn,
故答案为:an-bn;
(3)①29+28+27+…+23+22+2+1=(2-1)•(29+28•1+27•12+…+23•16+22•17+2•18)+1
=210-110+1
=210-1+1
=1024;
②210-29+28-…+23-22+2
=$\frac{1}{3}$×[2-(-1)]•[210×(-1)0+29×(-1)1+27×(-1)2+…+23×(-1)7+22×(-1)8+2×(-1)9+20×(-1)10-1]
=$\frac{1}{3}$[211-(-1)11-3]
=$\frac{1}{3}$×2046
=682.
点评 此题考查了数字的变化规律和多项式乘以多项式,弄清题中的规律是解本题的关键.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
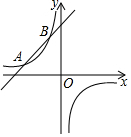 如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,
如图,一次函数的图象与反比例函数的图象交于A(-3,1)、B(m,3)两点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
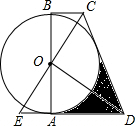 如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.
如图,AB为⊙O的直径,BC、AD是⊙O的切线,切点分别为B、A,过点O作EC⊥OD,EC交BC于点C,交AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )| A. | $\frac{17}{12}$π m2 | B. | $\frac{17}{6}$π m2 | C. | $\frac{25}{4}$π m2 | D. | $\frac{77}{12}$π m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
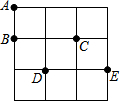 在3×3的方格纸中,点A,B,C,D,E分别位于如图所示的小正方形格点上.
在3×3的方格纸中,点A,B,C,D,E分别位于如图所示的小正方形格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com