
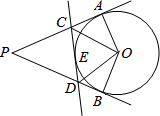
 已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.分析 (1)根据切线长定理得到PA=PB,AC=CE,BD=DE,根据三角形的周长公式计算即可;
(2)证明Rt△AOC≌Rt△EOC,得到∠AOC=∠COE和∠DOE=∠BOD,计算即可.
解答 解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°-90°-90°-50°=130°,
在Rt△AOC和Rt△EOC中,
$\left\{\begin{array}{l}{OA=OE}\\{OC=OC}\end{array}\right.$,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=$\frac{1}{2}$∠AOB=65°.
点评 本题考查的是切线长定理和全等三角形的判定和性质,掌握从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角是解题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
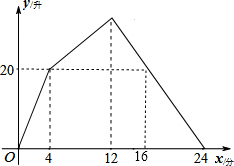 某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示
某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在地面向上空跑石块,石块终将落下 | |
| B. | 有一匹马以70米/秒的速度奔跑 | |
| C. | 杭州明年五一节当天的最高气温35℃ | |
| D. | 射击运动员射击一次,命中10环 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB>2CD | B. | AB=2CD | C. | AB<2CD | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com