
【题目】如图,E是正方形ABCD申CD边上任意一点.
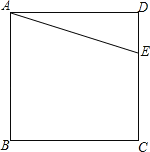
(1)以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形;
(2)在BC边上画一点F,使△CFE的周长等于正方形ABCD的周长的一半,请简要说明你取该点的理由.
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
将一个多位自然数分解为个位与个位之前的数,让个位之前的数减去个位数的两倍,若所得之差能被7整除,则原多位自然数一定能被7整除.也称这个数为“要塞数”.例如:将数1078分解为8和107,107﹣8×2=91,因为91能被7整除,所以1078能被7整除,就称1078为“要塞数”.
完成下列问题:
(1)若一个三位自然数是“要塞数”,且个位数字和百位数字都是7,则这个三位自然数位 ;
(2)若一个四位自然数M是“要塞数”,设M的个位数字为x,十位数字为y,且个位数字与百位数字的和为13,十位数字与千位数字的和也为13,记F(M)=|x﹣y|,求F(M)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0;②abc>0;③a+c>0;④9a+3b+c<0.其中,正确的结论有( )
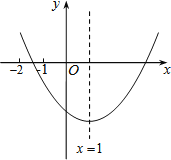
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.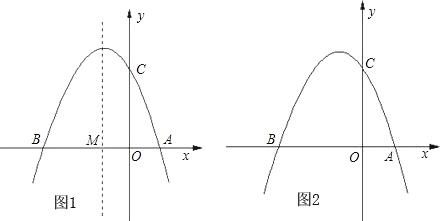
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到![]() ,
,![]() ).
).
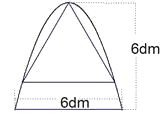
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,∠DCE=120°,当∠DCE的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
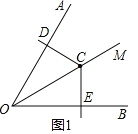
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;
(2)由(图1)的位置将∠DCE绕点C逆时针旋转θ角(0<θ<90°),线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com