
| A型车 | B型车 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
分析 (1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
解答 解:(1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由题意,得:
$\frac{50000}{x+400}$=$\frac{50000(1-20%}{x}$,
解得:x=1600,
经检验,x=1600是原方程的根.
答:今年A型车每辆售价1600元;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由题意,得
y=(1600-1100)a+(2000-1400)(60-a),
y=-100a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60-a≤2a,
∴a≥20.
∵y=-100a+36000.
∴k=-100<0,
∴y随a的增大而减小.
∴a=20时,y最大=34000元.
∴B型车的数量为:60-20=40辆.
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用、一次函数的解析式的运用,解答时由销售问题的数量关系求出一次函数的解析式是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
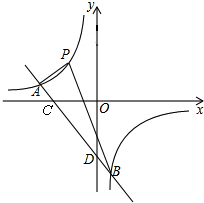 在反比例函数图象上且到x轴、y轴距离相等.
在反比例函数图象上且到x轴、y轴距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
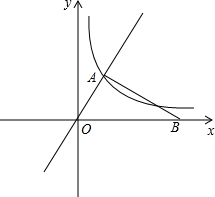 如图,在平面直角坐标系xOy中,已知直线y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.
如图,在平面直角坐标系xOy中,已知直线y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com