
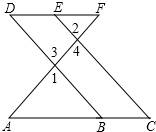
 完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.分析 首先根据对顶角知识得到∠3=∠4,即可判断出DB∥CE,利用平行线的性质即可得到∠D=∠ABD,由平行线的判定定理得到结论.
解答 证明:∵∠1=∠2(已知),∠1=∠3,∠2=∠4(对顶角相等)
∴∠3=∠4(等量代换)
∴DB∥CE(内错角相等,两直线平行)
∴∠C=∠ABD(两直线平行,同位角相等)
∴∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF(内错角相等,两直线平行),
故答案为对顶角相等;∠4;CE;内错角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行
点评 本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.


科目:初中数学 来源: 题型:解答题
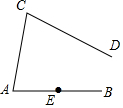 如图,已知∠ACD=75°,点E在AB上.
如图,已知∠ACD=75°,点E在AB上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,l ) | B. | (-2,-l ) | C. | (-1,-2 ) | D. | (-1,2 ) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
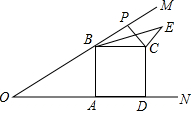 如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为2$\sqrt{3}$+2.
如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为2$\sqrt{3}$+2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -2 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填空,将本题补充完整.
填空,将本题补充完整.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com