
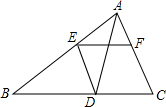
 如图,AD是△ABC的角平分线,DE∥AC,EF∥BC,若AB=15,AF=4,则DE的长等于6.
如图,AD是△ABC的角平分线,DE∥AC,EF∥BC,若AB=15,AF=4,则DE的长等于6. 分析 首先证明AE=DE;进而证明FC=DE;证明△AEF∽△ABC,列出比例式AE:AB=AF:AC,即可解决问题.
解答  解:∵DE∥AC,
解:∵DE∥AC,
∴∠CAD=∠EDA;
又∵∠EAD=∠DAC,
∴∠EDA=∠EAD,
∴ED=EA;
因为DE∥AC,EF∥BC,
∴四边形DCFE是平行四边形,
∴ED=FC;
设ED=EA=FC=x,
∵EF∥BC,
∴△AEF∽△ABC,
∴AE:AB=AF:AC,
∴x:15=4:(4+x),
∴x=6或x=-10(舍去),
∴DE=6,
故答案为:6.
点评 本题考查相似三角形的判定及其性质,平行四边形的判定,等腰三角形的判定及其性质等几何知识点的应用问题;对综合的分析问题解决问题的能力提出了较高的要求.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
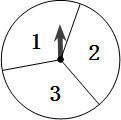 有一个转盘如图所示被平均分成3份,分别标有数字1、2、3,转盘上有一固定指针.转动转盘,当转盘停止时,指针指向哪一个数字即为转出的数字(若指针指向两个扇形的交线时,重新转动转盘).两人进行游戏,一人转动转盘,另一人掷骰子同时按所选方案的规则猜数(骰子的六个面分别标有数字1、2、3、4、5、6).如果猜出的数与所选方案的结果相符,则猜数的人获胜,否则,转盘的人获胜.猜数游戏有下列两种方案:
有一个转盘如图所示被平均分成3份,分别标有数字1、2、3,转盘上有一固定指针.转动转盘,当转盘停止时,指针指向哪一个数字即为转出的数字(若指针指向两个扇形的交线时,重新转动转盘).两人进行游戏,一人转动转盘,另一人掷骰子同时按所选方案的规则猜数(骰子的六个面分别标有数字1、2、3、4、5、6).如果猜出的数与所选方案的结果相符,则猜数的人获胜,否则,转盘的人获胜.猜数游戏有下列两种方案:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{24}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
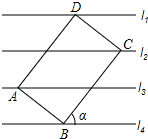 已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=6,BC=8,则tanα的值等于( )
已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=6,BC=8,则tanα的值等于( )| A. | 2:3 | B. | 3:4 | C. | 4:3 | D. | 3:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
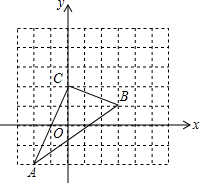 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com