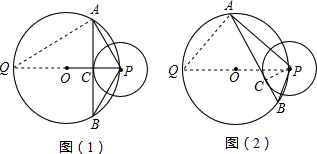
(1)证明:延长PO交⊙O于点Q,
连接AQ,如图(1),
∵AB与⊙P相切于点C,且PC是⊙P的半径,
∴AB⊥PC,即∠PCB=90°.
又∵PQ是⊙O的直径,
∴∠PAQ=90°.
∵∠PQA=∠PBC,
∴Rt△PAQ∽Rt△PCB,
∴

,
即PA•PB=PQ•PC.
又∵PQ=2R,PC=r,
∴PA•PB=2Rr;
(2)解:(1)中的结论成立.
证明:连接PO并延长交⊙O于点Q,
连接AQ,PC,如图(2),
由已知条件,得
∠PAQ=∠PCB=90°.
又∠PQA=∠PBC,
∴Rt△PAQ∽Rt△PCB,
∴

,
即PA•PB=PQ•PC=2Rr;
(3)解:PA•PB=2Rr.
分析:(1)本题很明显是用射影定理来证明.延长PO交⊙O于点Q,连接AQ.根据射影定理有PA
2=2Rr,根据垂径定理,可知PA=PB,由此可得证;
(2)结果不变.连接PC,过P作圆O的直径PQ,连接AQ,证△PCB∽△PAQ即可.
(3)结论不变,思路同(2).
点评:本题考查了圆与圆的位置关系、圆周角定理、相似三角形的判定和性质等知识点.

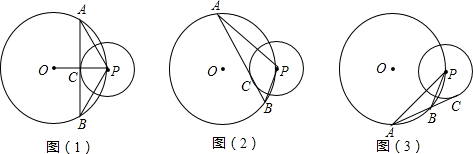
 (1)证明:延长PO交⊙O于点Q,
(1)证明:延长PO交⊙O于点Q, ,
, ,
,


 点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2