
����Ŀ���Ķ�������Լ������ƽ��ֱ������ϵ�У�����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ�ߣ��иõ�ġ������ߡ������磬��M��1��3�����������У�x=1��y=3��y=x+2��y=��x+4��
������̽������ͼ����ƽ��ֱ������ϵ����������OABC����B�ڵ�һ���ޣ�A��C�ֱ���x���y���ϣ������� ![]() ����B��C���㣬����D���������ڲ���
����B��C���㣬����D���������ڲ���
��1��ֱ��д����D��m��n�����е������ߣ�
��2������D��һ����������y=x+1����������ߵĽ���ʽ��
��3����P��AB���ϳ���A�������һ�㣬����OP������OAP����OP�۵�����A���ڵ�A���λ�ã�����A����ƽ�����������D�����������ʱ�����㣨2��������������������ƽ�ƶ��پ��룬�䶥������OP�ϣ�
���𰸡�
��1��
�⣺�ߵ�D��m��n����
���D��m��n������������x=m��y=n��y=x+n��m��y=��x+m+n
��2��
�⣺��D��һ����������y=x+1��
��n��m=1��
��n=m+1
�������߽���ʽΪ ![]() ��
��
��y= ![]() ��x��m��2+m+1��
��x��m��2+m+1��
���ı���OABC�������Σ���D��Ϊ�����εĶԳ��ᣬD��m��n����
��B��2m��2m����
�� ![]() ��2m��m��2+n=2m����n=m+1����õ�m=2��n=3��
��2m��m��2+n=2m����n=m+1����õ�m=2��n=3��
��D��2��3����
�������߽���ʽΪy= ![]() ��x��2��2+3
��x��2��2+3
��3��
�⣺��ͼ������A����ƽ����y���D���������ʱ��

��������ɵã�D��2��3����
��OA��=OA=4��OM=2��
���A��OM=60�㣬
���A��OP=��AOP=30�㣬
��MN= ![]() ��
��
����������Ҫ����ƽ�Ƶľ���=3�� ![]() =
= ![]() ��
��
��ͷ������A����ƽ����x���D���������ʱ��

�߶�������OP�ϣ�
��A����D�غϣ�
��A�䣨2��3����
��P��4��c����c��0����
���۵��У�PD=PA��
�� ![]() =c��
=c��
��c= ![]() ��
��
��P��4�� ![]() ��
��
��ֱ��OP����ʽΪy= ![]() ��
��
��N��2�� ![]() ����
����
����������Ҫ����ƽ�Ƶľ���=3�� ![]() =
= ![]() ��
��
��������������ƽ�� ![]() ��
�� ![]() ���룬�䶥������OP��
���룬�䶥������OP��
����������1������������ֱ�������D�������ߣ�
��2���ɵ�D��һ�������ߺ������ε����������D�����꣬�Ӷ���������߽���ʽ��
��3����ƽ����x���y��������������۵������ʼ��㼴�ɣ������Ƕ��κ����ۺ��⣬��Ҫ�������۵������ʣ������ε����ʣ������ߵ����⣬�Ȿ��Ĺؼ����������ε����������D�����꣮
�����㾫�������������ε����ʺͷ��۱任���۵����⣩�ǽ����ĸ�������Ҫ֪���������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ��۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=x+m��ͼ���뷴��������y= ![]() ��ͼ����A��B���㣬����x�ύ�ڵ�C����A������Ϊ��2��1����
��ͼ����A��B���㣬����x�ύ�ڵ�C����A������Ϊ��2��1���� 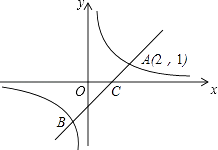
��1����m��k��ֵ��
��2�����C�����꣬�����ͼ��д������ʽ��0��x+m�� ![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱߡ�ABC��AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ���������ٶȶ�Ϊ1cm/s������AQ��CP���ڵ�M�������ĸ�����:��BP��CM���ڡ�ABQ�ա�CAP���ۡ�CMQ�Ķ������䣬ʼ�յ���60�㣻�ܵ���![]() ����
����![]() ��ʱ����PBQΪֱ�������Σ���ȷ���м��� ( )
��ʱ����PBQΪֱ�������Σ���ȷ���м��� ( )

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C=Rt����AB=5cm��BC=3cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��1cm���������ʱ��Ϊt�룮
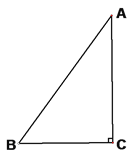
��1������2������ABP���ܳ���
��2����t����ʲô����ʱ����BCPΪֱ�������Σ�
��3������һ��Q���ӵ�C��ʼ����C��B��A��C��·���˶������ٶ�Ϊÿ��2cm����P��Q����ͬʱ��������P��Q����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶�����tΪ��ֵʱ��ֱ��PQ�ѡ�ABC���ܳ��ֳ���ȵ������֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���¹���Ʒ�֣�ij���ƻ��¹���A��B����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����A����ĵ���Ϊ7Ԫ/�ã�����B�����������y��Ԫ���빺������x���ã�֮�������ͼ��ʾ�ĺ�����ϵ��
��1����y��x�ĺ�����ϵʽ��
��2�����ڹ���ƻ��У�B���������������35�ã���������A���������������ƹ�����ʹ�ܷ�����ͣ��������ͷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
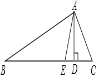
����Ŀ����֪����ͼ������ABC�У�AD��AE�ֱ�����ABC�ĸߺͽ�ƽ���ߣ�����B=40�㣬��EAD=15�㣮
���C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��ΪAB����C��Բ���ϣ�����A��B����AD��CD��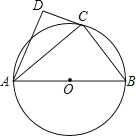
��1����BC=3��AB=5����AC��ֵ��
��2����AC�ǡ�DAB��ƽ���ߣ���֤��ֱ��CD�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
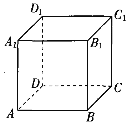
����Ŀ����ͼ����������ABCD��A1B1C1D1���ⳤΪ1���ڡ��������dz�ͬʱ�ӵ�A����������ͬ���ٶȷֱ�������ǰ���У��ڼdz����е�·����AA1��A1D1���������dz����е�·����AB��BB1�����������Ҷ���ѭ���¹��������еĵ�n��2���n�������ڵ�ֱ�߱����ǼȲ�ƽ��Ҳ���ཻ������n��������������ô���ڡ��������dz���������2018����ֱ�ֹͣ�������������嶥�㴦ʱ������֮��ľ������� ��
A. 0 B. ![]() C.
C. ![]() D. 1
D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ���ڽ�����һ���ڽǵ�3��ʱ�����dzƴ�������Ϊ�����������Ρ������һ�������������Ρ���һ����Ϊ108�㣬��ô��������������Ρ�����С�ڽǵĶ���Ϊ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com