
 交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线
交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线 经过点A、B、C.
经过点A、B、C.
 时,求点P的坐标;
时,求点P的坐标;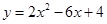 ;(2)P(1,2);(3)
;(2)P(1,2);(3)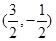
 交x轴、y轴的交点A、B的坐标,即可求得点C的坐标,最后根据点A、B、C在抛物线
交x轴、y轴的交点A、B的坐标,即可求得点C的坐标,最后根据点A、B、C在抛物线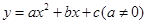 上,即可求得结果;
上,即可求得结果; ,
,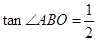 得
得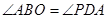 ,即可证得△ABO∽△ADP,根据相似三角形的性质可得AP的长,过点P作
,即可证得△ABO∽△ADP,根据相似三角形的性质可得AP的长,过点P作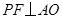 于点F,可证PF∥BO,即可证得
于点F,可证PF∥BO,即可证得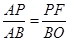 ,从而求得结果;
,从而求得结果; ,即可得到
,即可得到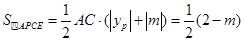 ,由
,由 即可列方程求解.
即可列方程求解. 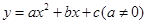 上,
上,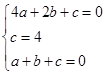 ,解得
,解得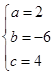
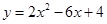 ;
; ,
,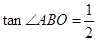 (
( 为锐角)
为锐角)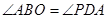 ,
, 
 ,
,  ,AD=5
,AD=5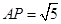
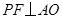 于点F,可证PF∥BO,
于点F,可证PF∥BO,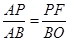

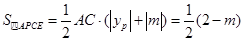
 得
得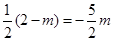 ,解得
,解得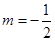
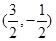 .
.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源:不详 题型:解答题
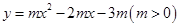 与
与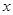 轴交于
轴交于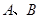 两点,与
两点,与 轴交于
轴交于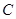 点.
点.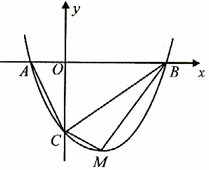
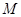 的坐标(用含
的坐标(用含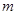 的代数式表示),
的代数式表示),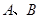 两点的坐标;
两点的坐标;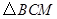 与
与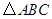 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;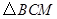 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
| 销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
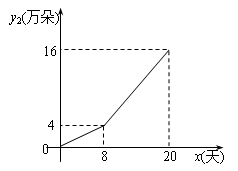
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
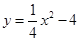 交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
交x轴于点Q、M,交y轴于点P,点P关于x轴的对称点为N。
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 交
交 轴于点
轴于点 ,交
,交 轴于点
轴于点 ,在
,在 轴上方的抛物线上有两点
轴上方的抛物线上有两点 ,它们关于
,它们关于 轴对称,点
轴对称,点 在
在 轴左侧.
轴左侧. 于点
于点 ,
, 于点
于点 ,四边形
,四边形 与四边形
与四边形 的面积分别为6和10,则
的面积分别为6和10,则 与
与 的面积之和为 .
的面积之和为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com