
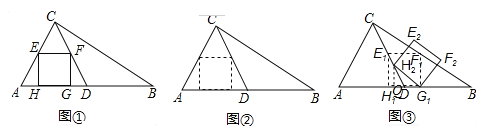
【题目】(2016湖南省益阳市)如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为![]() 时,求矩形平移的距离;
时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.

【答案】答案见解析.
【解析】试题分析:(1)根据已知,由直角三角形的性质可知AB=2,从而求得AD,CD,利用中位线的性质可得EF,DF,利用三角函数可得GF,由矩形的面积公式可得结果;
(2)首先利用分类讨论的思想,分析当矩形与△CBD重叠部分为三角形时(0<x≤![]() ),利用三角函数和三角形的面积公式可得结果;当矩形与△CBD重叠部分为直角梯形时(
),利用三角函数和三角形的面积公式可得结果;当矩形与△CBD重叠部分为直角梯形时(![]() <x≤
<x≤![]() ),列出方程解得x;
),列出方程解得x;
(3)作H2Q⊥AB于Q,设DQ=m,则H2Q=![]() ,又
,又![]() ,
,![]() ,利用勾股定理可得m,在Rt△QH2G1中,利用三角函数解得cosα.
,利用勾股定理可得m,在Rt△QH2G1中,利用三角函数解得cosα.
试题解析:(1)如图①,在△ABC中,∵∠ACB=90°,∠B=30°,AC=1,∴AB=2,
又∵D是AB的中点,∴AD=1,CD=![]() AB=1,
AB=1,
又∵EF是△ACD的中位线,∴EF=DF=![]() ,
,
在△ACD中,AD=CD,∠A=60°,∴∠ADC=60°,
在△FGD中,GF=DFsin60°=![]() ,∴矩形EFGH的面积S=EFGF=
,∴矩形EFGH的面积S=EFGF=![]() =
=![]() ;
;
(2)如图②,设矩形移动的距离为x,则0<x≤![]() ;
;
当矩形与△CBD重叠部分为三角形时,则0<x≤![]() ,S=
,S=![]() ,∴x=
,∴x=![]() .(舍去);
.(舍去);
当矩形与△CBD重叠部分为直角梯形时,则![]() <x≤
<x≤![]() ,重叠部分的面积S=
,重叠部分的面积S=![]() ,∴x=
,∴x=![]() ,即矩形移动的距离为
,即矩形移动的距离为![]() 时,矩形与△CBD重叠部分的面积是
时,矩形与△CBD重叠部分的面积是![]() ;
;
(3)如图③,作H2Q⊥AB于Q,设DQ=m,则H2Q=![]() ,又
,又![]() ,
,![]() .
.
在Rt△H2QG1中,![]() ,解之得m=
,解之得m=![]() (负的舍去),
(负的舍去),
∴cosα=![]() =
=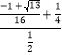 =
=![]() .
.


科目:初中数学 来源: 题型:
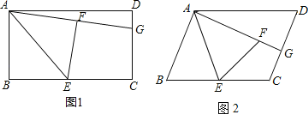
【题目】(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.
(2)简单应用:在(1)中,如果AB=4,AD=6,求DG的长;
(3)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
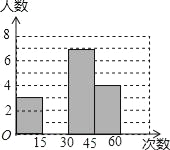
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:km)如下:-2 , +5 ,-1 ,+1 ,-6 ,- 2 ,问:
(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为0.2L/km(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
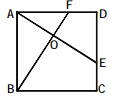
【题目】如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AC为直径,=,DE⊥BC,垂足为E.

(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若CE=1,AC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=![]() ,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
,BC=4.线段AB的垂直平分线DF分别交边AB、AC、BC所在的直线于点D、E、F.
(1)求线段BF的长;
(2)求AE:EC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足![]() ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com