
观察下列等式:
第1个等式: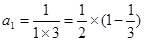 ;
;
第2个等式:
 ;
;
第3个等式:
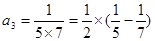 ;
;
第4个等式:
 ;
;
……
请解答下列问题:
(1)按以上规律列出第5个等式: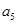 =
= ;
=
= ;
(2)用含有n的代数式表示第n个等式: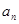 =
= (n为正整数);
=
= (n为正整数);
(3)求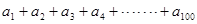 的值.
的值.
(1) ;
;
(2) =
=  =
= (n为正整数);
(n为正整数);
(3) .
.
【解析】
试题分析:仔细分析所给等式可知:第一个等号后面的式子规律是分子始终为1,分母是两个连续奇数的乘积;它们与式子序号之间的关系为:序号的2倍减1和序号的2倍加1;再应用所发现的规律解题即可.
(3)运用变化规律计算.
(1)按以上规律列出第5个等式: ;
;
(2)用含有n的代数式表示第n个等式:
 =
=  =
= (n为正整数);
(n为正整数);
(3)解:
= ×(1﹣
×(1﹣ )+
)+ ×(
×( ﹣
﹣ )+
)+ ×(
×( ﹣
﹣ )+
)+ ×(
×( ﹣
﹣ )+…+
)+…+ ×
×
···········3
= ×(1﹣
×(1﹣ +
+ ﹣
﹣ +
+ ﹣
﹣ +
+ ﹣
﹣ +…+
+…+ ﹣
﹣ )
)
= ×(1﹣
×(1﹣ )
)
= ×
×
= .
.
考点:本题考查的是寻找数字的规律及运用规律计算
点评:此类寻找规律的问题解答时大致可分为2个步骤:先寻找不变的和变化的;再发现变化的部分与序号的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7×9 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 9×11 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 11 |
| 1 |
| 9×11 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 11 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com