
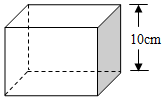
 如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?
如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?  全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
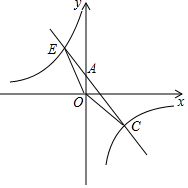 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax﹢b的图象交于C(4,-3),E(-3,4)两点.且一次函数图象交y轴于点A.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax﹢b的图象交于C(4,-3),E(-3,4)两点.且一次函数图象交y轴于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | △>M | B. | △=M | ||
| C. | △<M | D. | 无法确定△与M的大小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com