
【题目】对于任意两个实数对(a,b)和(c,d),规定:当且仅当a=c且b=d时, (a,b)=(c,d).定义运算“![]() ”:(a,b)
”:(a,b)![]() (c,d)=(ac-bd,ad+bc).若(1,2)
(c,d)=(ac-bd,ad+bc).若(1,2)![]() (p,3)=(q,q),则pq=___________.
(p,3)=(q,q),则pq=___________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3 cm,P、Q分别从B、A出发沿BC,AD方向运动,P点的运动速度是1 cm/秒,Q点的运动速度是2 cm/秒。连接AP并过Q作QE⊥AP垂足为E。
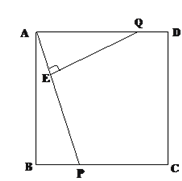
(1)求证:△ABP∽△QEA ;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时间t表示△QEA的面积y。(不要求考虑t的取值范围)
(提示:解答(2)(3)时可不分先后)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=12,AB=10,则AE的长为( )

A. 16B. 15C. 14D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
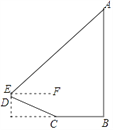
A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松雷中学图书馆近日购进甲、乙两种图书,每本甲图书的进价比每本乙图书的进价高20元,花780元购进甲图书的数量与花540元购进乙图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元?
(2)松雷中学计划购进甲、乙两种图书共70本,总购书费用不超过4000元,则最多购进甲种图书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】对于任意正实数a、b,因为![]() ≥0,所以
≥0,所以![]()
![]() ≥0,所以
≥0,所以![]() ≥2
≥2![]() ,只有当
,只有当![]() 时,等号成立.
时,等号成立.
【获得结论】在![]() ≥2
≥2![]() (a、b均为正实数)中,若
(a、b均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() ≥2
≥2![]() ,只有当
,只有当![]() 时,
时, ![]() 有最小值2
有最小值2![]() .
.
根据上述内容,回答下列问题:若![]() >0,只有当
>0,只有当![]() = 时,
= 时, ![]() 有最小值 .
有最小值 .
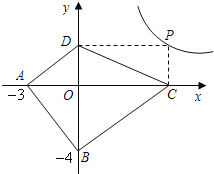
【探索应用】如图,已知A(-3,0),B(0,-4),P为双曲线![]() (
(![]() >0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方错误的是( )
A. x2+2x﹣99=0化为(x+1)2=100
B. 2x2﹣7x﹣4=0化为![]()
C. x2+8x+9=0化为(x+4)2=25
D. 3x2﹣4x﹣2=0化为(x-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
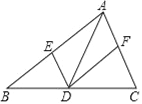
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com