
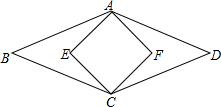
 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.  开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | m=$\frac{1}{2}$n | B. | m=$\frac{1}{4}$n | C. | m=$\frac{1}{2}$n2 | D. | m=$\frac{1}{4}$n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
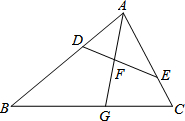 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:
为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 开口向上 | B. | 与x轴有两个重合的交点 | ||
| C. | 对称轴是直线x=1 | D. | 当x>1时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm,3cm,5cm | B. | 7cm,4cm,2cm | C. | 3cm,4cm,8cm | D. | 3cm,3cm,4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=20}\\{2x+y=12}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{x+2y=20}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=12}\\{2x+y=20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=12}\\{x+2y=20}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com