
分析 (1)当m=2时,方程化为x2-3x+3=0,然后计算判别式的值,根据判别式的意义判断方程根的情况;
(2)当m=-2时,方程化为x2+5x+3=0,然后利用配方法解方程.
解答 解:(1)当m=2时,方程化为x2-3x+3=0,
∵△=32-4×1×3=-4<0,
∴方程无实数根;
(2)当m=-2时,方程化为x2+5x+3=0,
(x+$\frac{5}{2}$)2=$\frac{13}{4}$
x+$\frac{5}{2}$=±$\frac{\sqrt{13}}{2}$,
所以x1=$\frac{\sqrt{13}-5}{2}$,x2=$\frac{-\sqrt{13}-5}{2}$.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.


科目:初中数学 来源: 题型:选择题
| 温度x/℃ | … | -4 | -2 | 0 | 2 | 4 | 4.5 | … |
| 植物每天高度增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 19.75 | … |
| A. | y=-x2-2x+49 | B. | y=-x2+2x+49 | C. | y=x2+2x-49 | D. | y=x2-2x+49 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
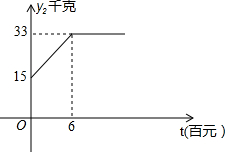 茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).
茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).| 型号 | A型包装 | B型包装 | C型包装 |
| 每盒装 | 龙井1千克 | 毛尖1千克 | 毛尖0.4千克;龙井0.6千克 |
| 每盒价格 | 45元 | 60元 | 56元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
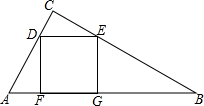 如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com