

分析 (1)设∠QPO=x,由QO=QP得到∠QPO=∠QOP=x,再根据三角形内角和定理得∠Q=180°-2x,由OQ=OC,得出∠C=180°-2x,再根据三角形外角性质得∠OPQ=∠C+∠POC,得180°-2x+30°=x,求得x的值,进而即可求得∠OCP的度数.
(2)分类讨论:如图2,设∠QOC=x,则∠QOP=x+30°,由QO=QP得到∠QPO=∠QOP=x+30°,再根据三角形外角性质得∠QCO=∠COP+∠CPO=x+60°,而OQ=OC,所以∠OQC=∠OCQ=x+60°,然后根据三角形内角和定理得x+x+60°+x+60°=180°,解得x=20°,再利用∠OCP=∠QOC+∠OQC进行计算即可;当点Q在C点时,则∠OCP=120°;利用同样的方法,解决如图3的情况.
解答  解:(1)如图1,设∠QPO=x,
解:(1)如图1,设∠QPO=x,
∵PQ=QO,
∴∠QOP=∠QPO=x,
∴∠Q=180°-2x,
∵OQ=OC,
∴∠C=180°-2x,
∵∠OPQ=∠C+∠POC,
∴180°-2x+30°=x,解得x=70°,
∴∠OCP=180°-2×70°=40°;
(2)存在,
如图2,设∠QOC=x,则∠QOP=x+30°,
∵QO=QP,
∴∠QPO=∠QOP=x+30°,
∴∠QCO=∠COP+∠CPO=30°+x+30°=x+60°,
∵OQ=OC,
∴∠OQC=∠OCQ=x+60°,
∴x+x+60°+x+60°=180°,解得x=20°,
∴∠OCP=∠QOC+∠OQC=20°+20°+60°=100°;
当点Q在C点时,易得∠OCP=120°;
如图3,设∠QPO=x,
∵PQ=QO,
∴∠QOP=∠QPO=x,
∴∠CQO=2x,
而OC=OQ,
∴∠C=2x,
∵∠AOC=∠APC+∠C,
∴x+2x=30°,解得x=10°,
∴∠OCP=2x=20°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的性质.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
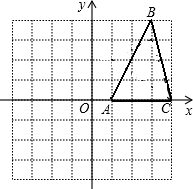 如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.
如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的直线ABC为甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(min)之间的函数关系的图象.由图象可知,通话2min需付电话费1.4元,通话5min需付电话费4.4元.
如图所示的直线ABC为甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(min)之间的函数关系的图象.由图象可知,通话2min需付电话费1.4元,通话5min需付电话费4.4元.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
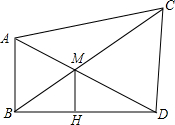 如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.
如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,b>0 | B. | a<0,b<0 | C. | a>0,b<0 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com