
【题目】如图,以点O为圆心,OE为半径作优弧EF,连接OE,OF,且OE=3,∠EOF=120°,在弧EF上任意取点A,B(点B在点A的顺时针方向)且使AB=2,以AB为边向弧内作正三角形ABC.
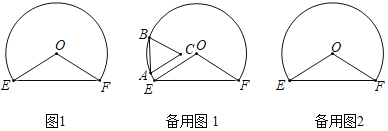
(1)发现:不论点A在弧上什么位置,点C与点O的距离不变,点C与点O的距离是 ;点C到直线EF的最大距离是 .
(2)思考:当点B在直线OE上时,求点C到OE的距离,在备用图1中画出示意图,并写出计算过程.
(3)探究:当BC与OE垂直或平行时,直接写出点C到OE的距离.
【答案】(1)![]() ;
;![]() ;(2)示意图见解析,点C到OE的距离为
;(2)示意图见解析,点C到OE的距离为![]() ;(3)当BC与OE垂直或平行时,点C到OE的距离为
;(3)当BC与OE垂直或平行时,点C到OE的距离为![]() 或
或![]() .
.
【解析】
(1)连接OB,OA,再连接OC并延长交AB于点G, 易知GO为线段AB的垂直平分线,通过勾股定理分别计算CG,GO的长,得到CO=GO-CG为定值即可;延长CO交EF于点H,当CO⊥EF时,点C到直线EF的距离最大,最大距离为CH的长,且CH=CO+OH,只需计算OH即可求出最大距离CH的长;
(2)过点C作OE的垂线,垂足为M,易证△OCM∽△OBG,得到![]() ,从而得到CM的长,即为点C到OE的距离;
,从而得到CM的长,即为点C到OE的距离;
(3)因为OC长不变,已求得,当BC与OE垂直或平行时,过点C作OE的垂线,利用OC不变,通过解相应的直角三角形,得到点C到OE的距离.
解:(1)如图1,连接OA、OB、OC,延长OC交AB于点G,

在正三角形ABC中,AB=BC=AC=2,
∵OA=OB,AC=BC,
∴OC垂直平分AB,
∴AG=![]() AB=1,
AB=1,
∴在Rt△AGC中,由勾股定理得:CG=![]() ,
,
在Rt△AGO中,由勾股定理得:OG=![]() ,
,
∴OC=![]() ;
;
如图2,延长CO交EF于点H,
当CO⊥EF时,点C到直线EF的距离最大,最大距离为CH的长,

∵OE=OF,CO⊥EF,
∴CO平分∠EOF,
∵∠EOF=120°,
∴∠EOH=![]() ∠EOF=60°,
∠EOF=60°,
在Rt△EOH中,cos∠EOH=![]() ,
,
∴cos60°=![]() =
=![]() ,
,
∴OH=![]() ,
,
∴CH=CO+OH=![]() ,
,
∴点C到直线EF的最大距离是![]() .
.
故答案为:![]() ;
;![]() .
.
(2)如图3,当点B在直线OE上时,过点C作OE的垂线,垂足为M
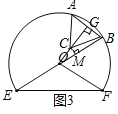
由OA=OB,CA=CB可知,
点O,C都在线段AB的垂直平分线上,
过点C作AB的垂线,垂足为G,
则G为AB中点,直线CG过点O.
∴由∠COM=∠BOG,∠CMO=∠BGO
∴△OCM∽△OBG,
∴![]() ,
,
∴![]() ,
,
∴CM=![]() ,
,
∴点C到OE的距离为![]() .
.
(3)如图4,当BC⊥OE时,设垂足为点M,

∵∠EOF=120°,
∴∠COM=180°﹣120°=60°,
∴在Rt△COM中,sin∠COM=![]() ,
,
∴sin60°=![]() =
=![]() ,
,
∴CM=![]() CO=
CO=![]() (
(![]() )=
)=![]() ;
;
如图5,当BC∥OE时,过点C作CN⊥OE,垂足为N,

∵BC∥OE,
∴∠CON=∠GCB=30°,
∴在Rt△CON中,sin∠CON=![]() ,
,
∴sin30°=![]() =
=![]() ,
,
∴CN=![]() CO=
CO=![]() (
(![]() )=
)=![]() ;
;
综上所述,当BC与OE垂直或平行时,点C到OE的距离为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】佳润商场销售![]() ,
,![]() 两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
|
| |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获 毛利润9万元.
(1)该商场计划购进![]() ,
,![]() 两种品牌的教学设备各多少套?
两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少![]() 种设备的购进数量,增加
种设备的购进数量,增加![]() 种设备的购进数量,已知
种设备的购进数量,已知![]() 种设备增加的数量 是
种设备增加的数量 是![]() 种设备减少的数量的1.5倍.若用于购进这两种教学设备的 总资金不超过69万元,问
种设备减少的数量的1.5倍.若用于购进这两种教学设备的 总资金不超过69万元,问![]() 种设备购进数量至多减少多少套?
种设备购进数量至多减少多少套?
(3)在(2)的条件下,该商场所能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
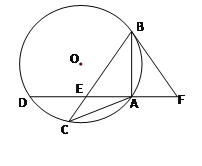
【题目】如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A, AD与 BC交于点E,F在DA的延长线上,且AF=AE.
(1)求证:BF是⊙O的切线;
(2)若AD=4,![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
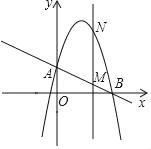
【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
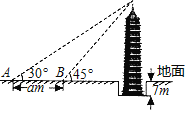
【题目】荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为_____米(![]() ≈1.73,结果精确到0.1).
≈1.73,结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.

(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .直线
.直线![]() 与
与![]()
![]()
![]() 交于点
交于点![]() .记线段
.记线段![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .横,纵坐标都是整数的点叫做整点.
.横,纵坐标都是整数的点叫做整点.
(1)当![]() 时,区域
时,区域![]() 内的整点个数为_____;
内的整点个数为_____;
(2)若区域![]() 内没有整点,则
内没有整点,则![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com