
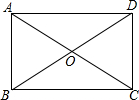
 如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.
如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长. 科目:初中数学 来源: 题型:填空题
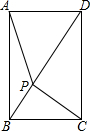 如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.
如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,BC=$\sqrt{3}$,则PA+PB+PC的最小值是$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
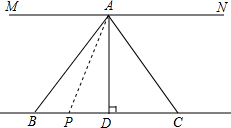 已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.
已知:如图,AD平分∠BAC,且AD⊥BC于点D,MN∥BC,请在括号中补全步骤的推理理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | C. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | D. | $\sqrt{(-4)^{2}}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某冷饮点一天售出各种口味雪糕数量的扇形统计图如图所示,其中售出红豆口味的雪糕200支.
某冷饮点一天售出各种口味雪糕数量的扇形统计图如图所示,其中售出红豆口味的雪糕200支.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | 1 | C. | 3 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
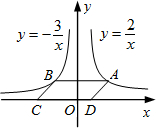 如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴并反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作?ABCD,其中点C,D在x轴上,则?ABCD的面积为( )
如图,点A是反比例函数y=$\frac{2}{x}$(x>0)的图象上任意一点,AB∥x轴并反比例函数y=-$\frac{3}{x}$的图象于点B,以AB为边作?ABCD,其中点C,D在x轴上,则?ABCD的面积为( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=17}\\{y=52}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=12}\\{y=23}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=8}\\{y=9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=9}\\{y=8}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com