
| b |
| 2 |
| t |
| t |
| t |
| t |
| b |
| 2 |
| t |
| t |
| t |
| t |
| t |
| t |
| t |
| t |



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
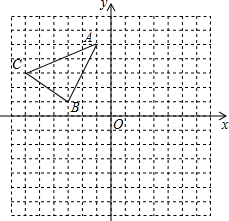 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§AΘ®-1Θ§5Θ©Θ§BΘ®-3Θ§1Θ©Θ§CΘ®-6Θ§3Θ©Θ°
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§AΘ®-1Θ§5Θ©Θ§BΘ®-3Θ§1Θ©Θ§CΘ®-6Θ§3Θ©Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
 ΓΨΈ Χβ«ιΨΒΓΩ
ΓΨΈ Χβ«ιΨΒΓΩ≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| ||||
|
2
|
|
| 45 |
|
| 3 |
| 2 |
2
|
| 2 |
| 1 |
| 2 |
| 6 |
| 8 |
| 4 |
| 3 |
| 18 |
| 8 |
| 1 |
| 3 |
| 54 |
| 3 |
| 12 |
| 18 |
|
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
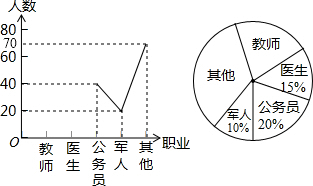
| AΓΔ±ΜΒς≤ιΒΡ―ß…ζ”–200»Υ |
| BΓΔ…»–ΈΆΦ÷–ΙΪΈώ‘±≤ΩΖ÷ΥυΕ‘”ΠΒΡ‘≤–ΡΫ«ΈΣ72Γψ |
| CΓΔ±ΜΒς≤ιΒΡ―ß…ζ÷–œ≤ΜΕΤδΥϊ÷Α“ΒΒΡ’Φ40% |
| DΓΔ±ΜΒς≤ιΒΡ―ß…ζ÷–œ≤ΜΕΫΧ Π÷Α“ΒΒΡ”–40»Υ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
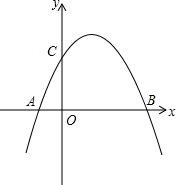 »γΆΦΘ§≈ΉΈοœΏy=
»γΆΦΘ§≈ΉΈοœΏy=| 1 |
| 2 |
| ||
| 2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
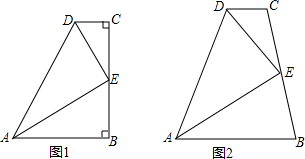
 »γΆΦΘ§“Μ¥ΈΚ· ΐy=-2x+12Ζ÷±π”κx÷αΓΔy÷αΫΜ”ΎΒψAΓΔBΘ§ΒψC «œΏΕΈABΒΡ÷–ΒψΘ§ΒψD‘ΎœΏΕΈOC…œΘ§«“OD=2CDΘ°
»γΆΦΘ§“Μ¥ΈΚ· ΐy=-2x+12Ζ÷±π”κx÷αΓΔy÷αΫΜ”ΎΒψAΓΔBΘ§ΒψC «œΏΕΈABΒΡ÷–ΒψΘ§ΒψD‘ΎœΏΕΈOC…œΘ§«“OD=2CDΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| 3 |
| x |
| 6 |
| 1-x |
| x+5 |
| x2-x |
| b |
| a2-ab |
| a |
| b2-ab |
| a2+b2 |
| a2b-ab2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com