
 如图,△ABC中AC=BC,D为边AB上的一点,且∠BCD=3∠ACD,O为AC上一点,以O为圆心的⊙O恰好经过C、D两点.
如图,△ABC中AC=BC,D为边AB上的一点,且∠BCD=3∠ACD,O为AC上一点,以O为圆心的⊙O恰好经过C、D两点.
 AB=3,则DM=AM-AD=3-2=1,
AB=3,则DM=AM-AD=3-2=1, ,即tan30°=
,即tan30°= ,
, =
= .
.

 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
 如图,△ABC中AC=BC,D为边AB上的一点,且∠BCD=3∠ACD,O为AC上一点,以O为圆心的⊙O恰好经过C、D两点.
如图,△ABC中AC=BC,D为边AB上的一点,且∠BCD=3∠ACD,O为AC上一点,以O为圆心的⊙O恰好经过C、D两点.查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区九年级第一学期期末考试数学试卷(解析版) 题型:选择题
如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上, C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )


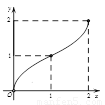


A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com