
【题目】如图,点E是正方形ABCD的边BC上一点,连接AE,将线段AE绕点E顺时针旋转一定的角度得到EF,点C在EF上,连接AF交边CD于点G.
(1)若AB=4,BF=8,求CE的长;
(2)求证:AE=BE+DG.

【答案】(1)EC=1;(2)证明见解析.
【解析】
(1)设AE=EF=x,由正方形的性质可知BE=8﹣x,AB=4,在![]() 中,根据勾股定理可得x的值,易求CE的长;
中,根据勾股定理可得x的值,易求CE的长;
(2)延长EB到H,使得BH=DG,则△ADG≌△ABE(SAS),由全等的性质及直角三角形的两锐角互余可证∠H=∠EAH,根据等角对等边可知EA=EH,易证结论.
(1)解:设AE=EF=x,
∵四边形ABCD是正方形,
∴∠ABE=90°,AB=BC=4,
∵BF=8,
∴CF=8﹣4=4,
∵BE=BF﹣EF=8﹣x,AB=4,AE=x,
∴x2=42+(8﹣x)2,
∴x=5,
∴EC=EF﹣CF=1.
(2)证明:延长EB到H,使得BH=DG,则△ADG≌△ABE(SAS),
∴∠BAH=∠DAG,
∴∠HAF=∠BAD=90°,
∵EF=AE,
∴∠EAF=∠F,
∵∠EAH+∠EAF=90°,∠F+∠H=90°,
∴∠H=∠EAH,
∴EA=EH,
∵EH=BE+BH=BE+DG,
∴AE=BE+DG.



科目:初中数学 来源: 题型:
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
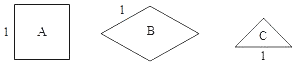
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),与y轴交于点B,且对称轴为x=1.
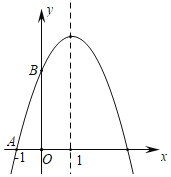
(1)求该抛物线的解析式;
(2)点P是抛物线对称轴上的一动点,当|PA﹣PB|取最大值时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
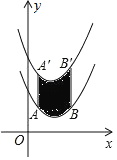
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图图形由大小相同的正方形组成,第1个图形小正方形的个数为5,第2个图形小正方形的个数为12,第3个图形小正方形的个数为21,则第6个图形小正方形的个数为( )
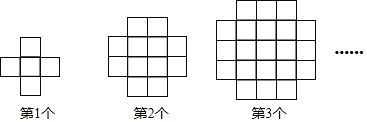
A.50B.60C.70D.80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(n,-1).
的图象与一次函数y=x+b的图象交于点A(1,4),点B(n,-1).
(1)求n和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
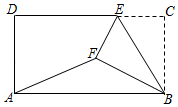
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.如图所示,图中点的横坐标表示科技馆从8:30开门后经过的时间(分钟),纵坐标表示到达科技馆的总人数.图中曲线对应的函数解析式为 ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
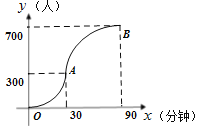
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,且∠A+∠ABC=90°,则∠PEF=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com