
分析 仿照例子,令S=1+5+52+53+…52017,则可得出5S=1+5+52+53+…52017+52018,两者做差后除以4即可得出结论.
解答 解:令S=1+5+52+53+…52017,
则5S=5+52+53+…52018,
∴S=$\frac{5S-S}{4}$=$\frac{{5}^{2018}-1}{4}$.
故答案为$\frac{{5}^{2018}-1}{4}$.
点评 本题考查了规律型中的数字的变化类,解题的关键是仿照例子计算1+3+32+33+…+32016.本题属于基础题,难度不大,本题其实是等比数列的求和公式,但初中未接触过该方面的知识,需要借助于错位相减法来求出结论.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
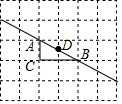 如图,在5×6的网格中,每个小正方形边长均为1,△ABC的顶点均为格点,D为AB中点,以点D为位似中心,相似比为2,将△ABC放大,得到△A′B′C′,则BB′=( )
如图,在5×6的网格中,每个小正方形边长均为1,△ABC的顶点均为格点,D为AB中点,以点D为位似中心,相似比为2,将△ABC放大,得到△A′B′C′,则BB′=( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{3\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{2}$或$\frac{3\sqrt{5}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
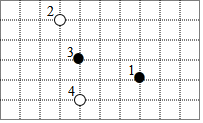 如图所示是围棋棋盘中的一部分,放置在某个平面直角坐标系中,白棋②的坐标是(-3,-1),白棋④的坐标是(-2,-5),则黑棋①的坐标是( )
如图所示是围棋棋盘中的一部分,放置在某个平面直角坐标系中,白棋②的坐标是(-3,-1),白棋④的坐标是(-2,-5),则黑棋①的坐标是( )| A. | (-3,-5) | B. | (0,0) | C. | (1,-4) | D. | (2,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com