
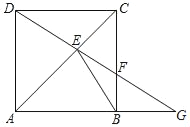
【题目】如图,四边形ABCD是矩形,E是对角线AC上的一点,EB=ED且∠ABE=∠ADE.
(1)求证:四边形ABCD是正方形;
(2)延长DE交BC于点F,交AB的延长线于点G,求证:EFAG=BCBE.
科目:初中数学 来源: 题型:
【题目】(10分)2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题

(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在数轴上,点A表示的数为-10,点B表示的数为14,点C到点A和点B之间的距离相等.
![]()
(1)求A,B两点之间的距离;
(2)求C点对应的数;
(3)甲、乙分别从A,B两点同时相向运动,甲的速度是1个单位长度/s,乙的速度是2个单位长度/s,求相遇点D对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
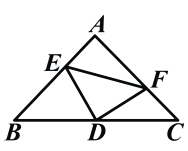
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的高速发展,计算机技术已是每位学生应该掌握的基本技能.为了提高学生对计算机的兴趣,老师把甲、乙两组各有10名学生,进行电脑汉字输入速度比赛,各组参赛学生每分钟输入汉字个数统计如下表:
输入汉字(个) | 132 | 133 | 134 | 135 | 136 | 137 |
甲组人数(人) | 1 | 0 | 1 | 5 | 2 | 1 |
乙组人数(人) | 0 | 1 | 4 | 1 | 2 | 2 |
(1)请你填写下表中甲班同学的相关数据.
组 | 众数 | 中位数 | 平均数( | 方差( |
甲组 | ||||
乙组 | 134 | 134.5 | 135 | 1.8 |
(2)若每分钟输入汉字个数136及以上为优秀,则从优秀人数的角度评价甲、乙两组哪个成绩更好一些?
(3)请你根据所学的统计知识,从不同角度评价甲、乙两组学生的比赛成绩(至少从两个角度进行评价).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
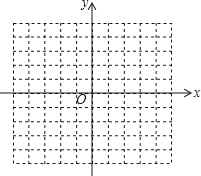
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠C=90°,DC=5,以CD为半径的⊙C与以AB为半径的⊙B相交于点E、F,且点E在BD上,联结EF交BC于点G.
(1)设BC与⊙C相交于点M,当BM=AD时,求⊙B的半径;
(2)设BC=x,EF=y,求y关于x的函数关系式,并写出它的定义域;
(3)当BC=10时,点P为平面内一点,若⊙P与⊙C相交于点D、E,且以A、E、P、D为顶点的四边形是梯形,请直接写出⊙P的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
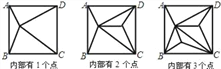
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2008个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
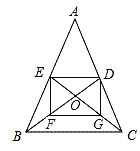
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com