
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{5}$ |
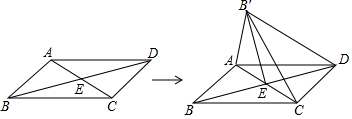
分析 如图,连接BB′.根据折叠的性质知△BB′E是等腰直角三角形,则BB′=$\sqrt{2}$BE.又B′E是BD的中垂线,则DB′=BB′.
解答 解: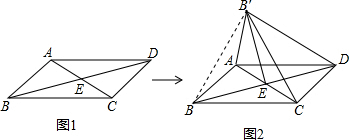 ∵四边形ABCD是平行四边形,BD=4,
∵四边形ABCD是平行四边形,BD=4,
∴BE=$\frac{1}{2}$BD=2.
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,则BB′=$\sqrt{2}$BE=2$\sqrt{2}$.
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=2$\sqrt{2}$.
故选A.
点评 此题考查了平行四边形的性质以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:填空题
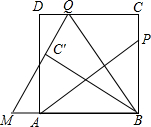 如图,P为正方形ABCD的边BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′,交BA的延长线于点M,当AB=3,BP=2PC时,QM=$\frac{13}{4}$.
如图,P为正方形ABCD的边BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′,交BA的延长线于点M,当AB=3,BP=2PC时,QM=$\frac{13}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.075 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com