
| A. | n2+2 | B. | -n2+2 | C. | n2-2 | D. | -n2-2 |
分析 把$\frac{β}{α}$+$\frac{α}{β}$化为$\frac{(α+β)^{2}-2αβ}{αβ}$求解即可.
解答 解:∵方程x2+nx-1=0的两实数根分别为α、β,
∴α+β=-n,αβ=-1
∴$\frac{β}{α}$+$\frac{α}{β}$=$\frac{{α}^{2}+{β}^{2}}{αβ}$=$\frac{(α+β)^{2}-2αβ}{αβ}$=$\frac{{n}^{2}+2}{-1}$=-n2-2,
故选:D.
点评 本题主要考查了根与系数的关系,解题的关键是$\frac{β}{α}$+$\frac{α}{β}$化为$\frac{(α+β)^{2}-2αβ}{αβ}$.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当a≠±1时,原方程是一元二次方程 | B. | 当a≠1时,原方程是一元二次方程 | ||
| C. | 当a≠-1时,原方程是一元二次方程 | D. | 原方程是一元二次方程 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
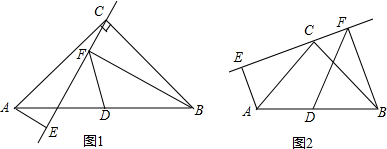
 如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.
如图,在△ABC中,AC⊥BC,CE⊥AB于E,AF平分∠CAB交CE于点F,过点F作FD∥BC交AB于点D,说明AC=AD成立的理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
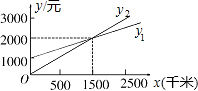 某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司的一家签定月租车合同,设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公司的月费是y2元,yl、y2分别与x之间的函数关系图象 (两条射线)如图所示,当每月行驶的路程等于1500时,租两家的费用相同?
某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司的一家签定月租车合同,设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公司的月费是y2元,yl、y2分别与x之间的函数关系图象 (两条射线)如图所示,当每月行驶的路程等于1500时,租两家的费用相同?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com