
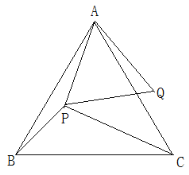
【题目】已知,点P是等边△ABC内一点,PA=4,PB=3,PC=5.线段AP绕点A逆时针旋转60°到AQ,连接PQ.(1)求PQ的长。(2)求∠APB的度数。
【答案】(1)4(2)150°
【解析】试题分析:(1)由旋转的性质可知AP=AQ,然后可证明△APQ为等边三角形,从而可求得PQ的长;
(2)先依据等边三角形的性质证明△APB≌△AQC,从而得到QC的长,然后依据勾股定理的逆定理证明△PQC为直角三角形,故此可求得∠AQC的度数,从而得到∠APB的度数.
解:(1)∵AP=AQ,∠PAQ=60°
∴△APQ是等边三角形,
∴PQ=AP=4.
(2)连接QC.

∵△ABC、△APQ是等边三角形,
∴∠BAC=∠PAQ=60°,
∴∠BAP=∠CAQ=60°﹣∠PAC.
在△ABP和△ACQ中![]() ,
,
∴△ABP≌△ACQ.
∴BP=CQ=3,∠APB=∠AQC,
∵在△PQC中,PQ2+CQ2=PC2
∴△PQC是直角三角形,且∠PQC=90°
∵△APQ是等边三角形,
∴∠AQP=60°
∴∠APB=∠AQC=60°+90°=150°.


科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F. 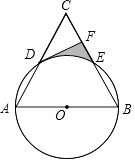
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度. 图1为点P在⊙O外的情形示意图.
(1)若点B(1,0),C(1,1), ![]() ,则SB=;SC=;SD=;
,则SB=;SC=;SD=;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR , 直接写出满足条件的线段PQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC与BD相交于O,不能判定四边形ABCD是平行四边形的是( )
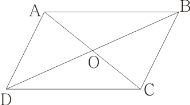
A. AB∥CD,AO=CO B. AB∥DC,∠ABC=∠ADC
C. AB=DC,AD=BC D. AB=DC,∠ABC=∠ADC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com