
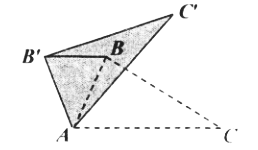
【题目】如图,在![]() 中,
中,![]() ,以点A为旋转中心,将
,以点A为旋转中心,将![]() 绕点A逆时针旋转,得
绕点A逆时针旋转,得![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的大小是( )
的大小是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据旋转的性质得AB′=AB,∠B′A C′=∠BAC,再根据等腰三角形的性质得∠AB′B=∠ABB′,然后根据平行线的性质由BB′∥AC得∠ABB′=∠CAB=65°,则∠AB′B=∠ABB′=65°,再根据三角形内角和计算出∠BAB′=50°,所以∠BAC′=15°.
解:∵△ABC绕点A逆时针旋转到△AB′C′的位置,
∴AB′=AB,∠B′A C′=∠BAC=![]() ,
,
∴∠AB′B=∠ABB′,
∵BB′∥AC,
∴∠ABB′=∠CAB=65°,
∴∠AB′B=∠ABB′=65°,
∴∠BAB′=180°-2×65°=50°,
∴∠BAC′=∠B′A C′-∠BAB′=65°-50°=15°,
故选:A.


科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为半圆的直径,点
为半圆的直径,点![]() 为圆心,
为圆心,![]() 为半圆的切线,过半圆上的点
为半圆的切线,过半圆上的点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)连接![]() ,若
,若![]() ,求证:
,求证:![]() 是半圆的切线;
是半圆的切线;
(2)如图2,当线段![]() 与半圆交于点
与半圆交于点![]() 时,连接
时,连接![]() ,
,![]() ,判断
,判断![]() 和
和![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组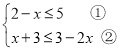
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_____________________;
(Ⅱ)解不等式②,得_____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月12日是我国义务植树节。某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了不完整的扇形统计图和条形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形统计图中m的值是_____________,补全条形统计图
(Ⅱ)求抽取的这部分学生植树棵数的平均数;
(Ⅲ)若本次活动共有320名学生参加,估计植树棵数超过8棵的约有多少人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() .有下列结论:①
.有下列结论:①![]() ; ②当
; ②当![]() 时,随x的增大而增大;③当
时,随x的增大而增大;③当![]() 时,
时,![]() ;④当
;④当![]() 时,若二次函数的最小值为
时,若二次函数的最小值为![]() ,则m的取值范围是
,则m的取值范围是![]() 。其中正确结论的个数是( )
。其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
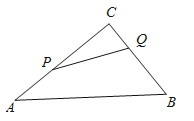
【题目】如图,△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.
(1)经过几秒,△CPQ的面积等于3cm2?
(2)在整个运动过程中,是否存在某一时刻t,使PQ恰好平分△ABC的面积?若存在,求出运动时间t;若不存在,请说明理由.
(3)是否存在某一时刻,PQ长为![]() ,如果存在,求出运动时间t。
,如果存在,求出运动时间t。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com