
【题目】如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )

A. 3 B. 4 C. 3![]() D. 4
D. 4![]()
科目:初中数学 来源: 题型:
【题目】如图1,点O是矩形ABCD的中心(对角线的交点),AB=4cm,AD=6cm.点M是边AB上的一动点,过点O作ON⊥OM,交BC于点N,设AM=x,ON=y,今天我们将根据学习函数的经验,研究函数值y随自变量x的变化而变化的规律.
下面是某同学做的一部分研究结果,请你一起参与解答:
(1)自变量x的取值范围是______;
(2)通过计算,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 2.40 | 2.24 | 2.11 | 2.03 | __ | __ | 2.11 | 2.24 | 2.40 |
请你补全表格(说明:补全表格时相关数值保留两位小数,参考数据:![]() ≈3.04,
≈3.04,![]() ≈6.09)
≈6.09)
(3)在如图2所示的平面直角坐标系中,画出该函数的大致图象.
(4)根据图象,请写出该函数的一条性质.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )

A. 1 m B. 2 m C. 3 m D. 6 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.

(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45° , BC=4,以AC为直角边,点A为直角顶点向△ABC的外侧作等腰直角三角形ACD,连接BD,则△DBC的面积为( ) .
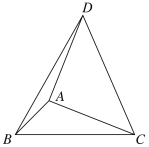
A.8B.10C.4![]() D.8
D.8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=60°,∠ACB=50°,延长CB至点D,使DB=BA,延长BC至点E,使CE=CA,连接AD,AE. 求∠DAE的度数
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.

(1)求直线AB的解析式;
(2)当点P运动到点(![]() ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;
(3)是否存在点P,使△OPD的面积等于![]() ?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
(1)求证:CD是⊙O的切线;
(2)E为![]() 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=
的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=![]() ,BE=BG,EG=3
,BE=BG,EG=3![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com