
分析 (1)直接利用积的乘方运算法则化简,进而利用单项式乘以单项式求出答案;
(2)直接利用平方差公式计算得出答案;
(3)直接利用完全平方公式计算得出答案;
(4)直接利用零指数幂的性质以及负整数指数幂的性质化简求出答案;
(5)利用平方差公式以及完全平方公式计算得出答案;
(6)利用单项式乘以单项式进而求出答案;
(7)直接利用平方差公式以及完全平方公式计算得出答案;
(8)直接利用平方差公式以及多项式乘法计算得出答案.
解答 解:(1)(-xy2z3)2(-x2y)3;
=x2y4z6•(-x6y3)
=-x8y7z6;
(2)(-$\frac{1}{4}$x-2y)(-$\frac{1}{4}$x+2y)
=$\frac{1}{16}$x2-4y2;
(3)(-2x+$\frac{1}{3}$y)2;
=4x2+$\frac{1}{9}$y2-$\frac{4}{3}$xy;
(4)(-1)2012+(-$\frac{1}{2}$)-2-(3.14-π)0
=1+4-1
=4;
(5)(x-y+1)(x+y-1)
=x2-(y-1)2
=x2-y2+2y-1;
(6)x2•x-4(-x)3+(-2x)(-3x2)
=x3+4x3+6x3
=11x3;
(7)(x+y)2-3(y-2x)(y-2x)
=x2+y2-3(y2+4x2-4xy)
=-2y2-11x2+12xy;
(8)(2x-5)(2x+5)-(2x+1)(2x-3)
=4x2-25-(4x2-6x+2x-3)
=4x-22.
点评 此题主要考查了整式的混合运算以及实数运算等知识,熟练应用乘法公式是解题关键.


科目:初中数学 来源: 题型:解答题
 已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.
已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 调查奥运会金牌获得者的兴奋剂使用情况 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
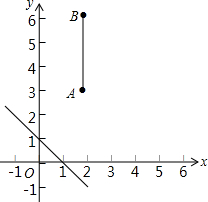 如果,在平面直角坐标系中,已知点A(2,3)、B(2,6),连接AB,如果点P在直线y=-x+1上,且点P到直线的距离小于1,那么点P是线段AB的“环绕点”,若点Q(m,n)是线段AB的“环绕点”,求n的取值范围.
如果,在平面直角坐标系中,已知点A(2,3)、B(2,6),连接AB,如果点P在直线y=-x+1上,且点P到直线的距离小于1,那么点P是线段AB的“环绕点”,若点Q(m,n)是线段AB的“环绕点”,求n的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-2=x | B. | x2-2x=2x | C. | x-2=2x | D. | x=2x-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
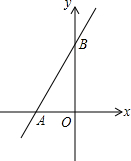 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com