
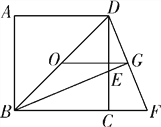
【题目】已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
(1)求证:△BCE≌△DCF;
(2)OG与BF有什么数量关系?证明你的结论;
(3)若GE·GB=4-2![]() ,求正方形ABCD的面积.
,求正方形ABCD的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】任何一个正整数![]() 都可以写成两个正整数相乘的形式,我们把两个乘数的差的绝对值最小的一种分解
都可以写成两个正整数相乘的形式,我们把两个乘数的差的绝对值最小的一种分解![]() 称为正整数
称为正整数![]() 的最佳分解,并定义一个新运算
的最佳分解,并定义一个新运算![]() .例如:12=1×12=2×6=3×4,则
.例如:12=1×12=2×6=3×4,则![]() .那么以下结论中:①F(2)=
.那么以下结论中:①F(2)=![]() ;②F(24)=
;②F(24)=![]() ;③若
;③若![]() 是一个完全平方效,则
是一个完全平方效,则![]() ;④若
;④若![]() 是一个完全立方数(即
是一个完全立方数(即![]() ,
,![]() 是正整数),则
是正整数),则![]() .正确的个数为( )
.正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
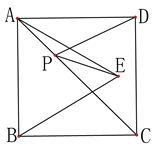
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )
A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.
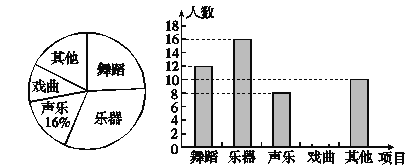
请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了__________名学生;
(2)请将最喜欢活动为 “戏曲”的条形统计图补充完整;
(3)你认为在扇形统计图中,“其他”所在的扇形对应的圆心角的度数是__________°;
(4)若该校共有3100名学生,请你估计全校对“乐器”最喜欢的人数是________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个四位自然数n,如果n满足各个数位上的数字互不相同且均不为0,它的千位数字与个位数字之和等于百位数字与十位数字之和,那么称这个数n为“平衡数”.对于一个“平衡数”,从千位数字开始顺次取出三个数字构成四个三位数,把这四个三位数的和与222的商记为F(n). 例如:n=1526,因为1+6=2+5,所以1526是一个“平衡数”,从千位数字开始顺次取出三个数字构成的四个三位数分别为152、526、261、615,这四个三位数的和为:152+526+261+615=1554,1154![]() 222=7,所以F(1526)=7.
222=7,所以F(1526)=7.
![]() 写出最小和最大的“平衡数”n,并求出对应的F(n)的值;
写出最小和最大的“平衡数”n,并求出对应的F(n)的值;
![]() 若s,t都是“平衡数”,其中s=10x+y+3201,t=1000m+10n+126(
若s,t都是“平衡数”,其中s=10x+y+3201,t=1000m+10n+126(![]() ,
, ![]() ,
, ![]() ,
, ![]() ,x, y, m, n都是整数),规定:
,x, y, m, n都是整数),规定: ![]() ,当F(s)+F(t)是一个完全平方数时,求k的最大值.
,当F(s)+F(t)是一个完全平方数时,求k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
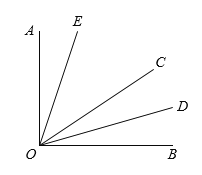
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在数轴上分别表示有理数![]() 、
、![]() ,在数轴上A、B两点之间的距离
,在数轴上A、B两点之间的距离![]() .
.

回答下列问题:
(1)数轴上表示1和![]() 的两点之间的距离是 ;
的两点之间的距离是 ;
(2)数轴上表示![]() 和
和![]() 的两点之间的距离表示为 ;
的两点之间的距离表示为 ;
(3)若![]() 表示一个有理数,请你结合数轴求
表示一个有理数,请你结合数轴求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
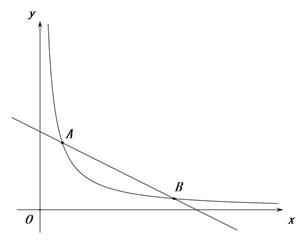
【题目】如图,一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6)和B(m,1)
(x>0)的图象交于点A(2,6)和B(m,1)
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com