
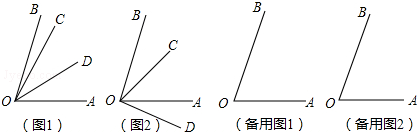
分析 根据题意和小明的分析,可以得到符合要求的还有三种情况,然后针对存在的三种情况,画出相应的图形,然后进行计算,即可得到∠BOC的度数,从而可以解答本题.
解答 解:(1)②如下图2所示,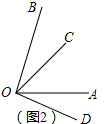
设∠BOC=α,则∠BOD=3α,∠COD=∠BOD-∠BOC=2α,
∵∠AOD=$\frac{1}{2}$∠AOC,
∴∠AOD=$\frac{1}{3}$∠COD=$\frac{2}{3}α$,
∴∠AOB=∠BOD-∠AOD=3α$-\frac{2α}{3}$=$\frac{7α}{3}$=70°,
∴α=30°.
∴∠BOC=30°;
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD=$\frac{1}{2}$∠AOC,
∴射线OD的位置也只有两种可能;
①若射线OD在∠AOB内部,如图3所示,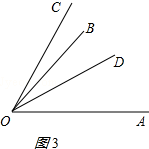
∵∠COD=∠BOC+∠BOD=4α,
∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
∴∠BOC=10°;
②若射线OD在∠AOB外部,如图4所示,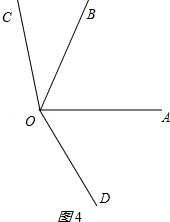
∵∠COD=∠BOC+∠BOD=4α,∠AOD=$\frac{1}{2}$∠AOC,
∴∠AOD=$\frac{1}{3}$∠COD=$\frac{4}{3}$α,
∴∠AOB=∠BOD-∠AOD=3α-$\frac{4}{3}α$=$\frac{5}{3}α$=70°,
∴α=42°,
∴∠BOC=42°;
由上可得,∠BOC的度数分别是14°,30°,10°,42°.
故答案为:14°,30°,10°或42°.
点评 本题考查角的计算,解题的关键是明确题意,利用数形结合和分类讨论的数学思想解答问题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $-\sqrt{25}$ | C. | -2.171171117 | D. | $\root{3}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 14 | D. | 14.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
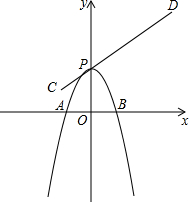 如图,抛物线与x轴相交于A、B两点,在保持抛物线的形状与大小不变的前提下,顶点P在线段CD上移动,点C、D的坐标分别为(-1,1)和(3,4).当顶点P移动到点C时,点B恰好与原点重合.在整个移动过程中,点A移动的距离为( )
如图,抛物线与x轴相交于A、B两点,在保持抛物线的形状与大小不变的前提下,顶点P在线段CD上移动,点C、D的坐标分别为(-1,1)和(3,4).当顶点P移动到点C时,点B恰好与原点重合.在整个移动过程中,点A移动的距离为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |
| B. |
| ||||||||||||||||||||||
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com