
分析 (1)直接利用待定系数法确定函数关系式进而得出答案;
(2)根据题意得出W与x之间的关系式,进而求出最大利润.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{80k+b=70}\\{70k+b=80}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=150}\end{array}\right.$,
所求一次函数的表达式为y=-x+150;
(2)W=(x-60)(-x+150)
=-x2+210x-9000
=-(x-105)2+2025
∵a=-1,
∴当x<105时,W随x的增大而增大,
又∵销售单价不低于成本单价,且获利不得高于40%,
∴60≤x≤60×(1+40%),即60≤x≤84,
∴当x=84时,W取得最大值为:-(84-105)2+2025=1584.
∴当销售单价定为84元时,商场可获得最大利润,最大利润是1584元.
点评 此题主要考查了二次函数的应用,正确得出二次函数关系式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 筹款金额(元) | 10 | 15 | 20 |
| 人数 | 10 | 17 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
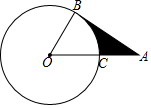 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径是4,则阴影部分面积是8$\sqrt{3}$-$\frac{8}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com