

分析 (1)由正方形得对边平行,由平行得△ADF∽△EBF,列比例式可得DF=2BF;
(2)如图②,延长DC、AB交于M,先证明△CEM≌△BEA,CM=AB,即DM=2AB,再证明△DHM∽△GHA,列比例式可得结论;
(3)如图③,作辅助线,构建相似三角形,同理证明△CGO≌△BGA,列比例式可得所求的比值.
解答  解:(1)如图①,∵四边形ABCD为正方形,
解:(1)如图①,∵四边形ABCD为正方形,
∴AD∥BC,AD=BC,
∵E是BC的中点,
∴BC=2BE,
∵AD∥BC,
∴△ADF∽△EBF,
∴$\frac{DF}{BF}=\frac{AD}{BE}$,
∴$\frac{DF}{BF}=\frac{BC}{BE}$=$\frac{2}{1}$,
∴DF=2BF;
故答案为:DF=2BF;
(2)如图②,延长DC、AE交于M,
∵DC∥AB,
∴∠ABC=∠ECM,∠M=∠EAB,
∵CE=BE,
∴△CEM≌△BEA,
∴CM=AB,
∵G是AB的中点,
∴AG=BG,
设AG=x,则AB=2x,DM=4x,
∵DM∥AB,
∴△DHM∽△GHA,
∴$\frac{DM}{AG}=\frac{DH}{HG}$,
∴$\frac{4x}{x}$=$\frac{DH}{HG}$,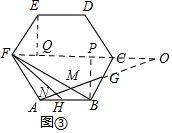
∴$\frac{DH}{HG}$=4;
(3)如图③,连接FC并延长,交AG的延长线于O,过B作BP⊥OF于P,过E作EQ⊥OF于Q,
在正六边形ABCDEF中,
∴∠ABC=180°-$\frac{360°}{6}$=120°,AB=BC,
∴∠PBC=120°-90°=30°,∠FCB+∠ABC=180°,
∴FC∥AB,PC=$\frac{1}{2}$BC,
同理FQ=$\frac{1}{2}$EF,
∵点H、G分别是AB、BC的中点,
∴AH=BH=$\frac{1}{2}$AB,BG=CG=$\frac{1}{2}$BC,
设AH=x,则BC=AB=2x,
∴FC=4x,
∵FC∥AB,
∴∠O=∠GAB,
∵BG=CG,∠CGO=∠BGA,
∴△CGO≌△BGA,
∴CO=AB=2x,
∴OF=6x,
∵OF∥AB,
∴△FNO∽△HNA,
∴$\frac{FN}{NH}=\frac{OF}{AH}$=$\frac{6x}{x}$,
∴$\frac{FN}{NH}$=6.
点评 本题是四边形的综合题,考查了正方形、正六边形的性质、平行相似的判定,本题的关键是作辅助线,构建平行相似的三角形;同时还运用了类比的思想,通过问题1的解决,启发了第2个和第3个问题的思路,利用作辅助线的方式使问题得以解决.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
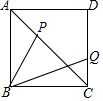 如图,正方形ABCD中,已知AB=2,动点P、Q分别在AC、CD上,且AP=CQ,则(BP+BQ)2的最小值是8+4$\sqrt{2}$.
如图,正方形ABCD中,已知AB=2,动点P、Q分别在AC、CD上,且AP=CQ,则(BP+BQ)2的最小值是8+4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下列推理说明:
完成下列推理说明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com