练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如果△ABC是等腰三角形，若周长是18，一边长是8，则另两边长是5，5或2，8．

    分析 由于已知长度的边没有指明是等腰三角形的底边还是腰，因此要分类讨论，最后要根据三角形三边关系定理判断求出的结果是否符合题意．

    解答 解：①当等腰三角形的底长为8时，腰长=（18-8）÷2=5；
    则等腰三角形的三边长为8、5、5；5+5＞8，能构成三角形．
    ②当等腰三角形的腰长为8时，底长=18-2×8=2；
    则等腰三角形的三边长为8、8、2；8+2＞8，亦能构成三角形．
    故等腰三角形另外两边的长为5，5或2，8．
    故答案为：5，5或2，8．

    点评 本题考查了等腰三角形的性质及三角形的三边关系；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．如果两个多边形仅有角分别相等，它们相似吗？如果仅有边成比例呢？若不一定相似，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

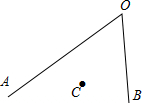    7．某班举行文艺晚会，桌子摆成两条直线（OA、OB），OA桌面上摆满了橘子，OB桌面摆满了糖果，坐在C处的小明先拿橘子再拿糖果，然后回到座位，请你帮助他设计路线，使其行走的总路程最短．（保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在Rt△ABC中，∠B=90°，点E是AC的中点，AC=2AB，∠BAC的平分线AD交BC于点D，作AF∥BC，连接DE并延长交AF于点F，连接FC．求证：AF=DA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．矩形的一个角的平分线分一边为3cm和4cm两部分，则这个矩形的对角线的长为$\sqrt{65}$或$\sqrt{58}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．（a-1）2+|b+2|=0，则（a+b）2015的值是-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．绝对值不大于5.1的整数有（　　）
    A．11个B．12个C．22个D．23个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．冷库的温度为+2℃，现存入一批食物冷冻，必须使室温保持在-22℃．若冷冻机可使室温每小时下降5℃，经过多少小时，就可以使冷库温度达到-22℃的冷冻温度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．平方等于本身的数是0，1，倒数等于本身的数是±1，绝对值最小的有理数是0．

    查看答案和解析>>

    同步练习册答案