
如图,抛物线 的对称轴是直线x=
的对称轴是直线x= ,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
(1)求抛物线的解析式;
(2)过点C作CD//x轴交抛物线于点D,连接AD交y轴于点E,连接AC,设△AEC的面积为S1, △DEC的面积为S2,求S1:S2的值;
(3)点F坐标为(6,0),连接D,在(2)的条件下,点P从点E出发,以每秒3个单位长的速度沿E→C→D→F匀速运动;点Q从点F出发,以每秒2个单位长的速度沿F→A匀速运动,当其中一点到达终点时,另外一点也随之停止运动.若点P、Q同时出发,设运动时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是直角三角形?请直接写出所有符合条件的t值..
解:(1)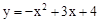
(2)
(3)当 时,以D、P、Q为顶点的三角形是直角三角形。
时,以D、P、Q为顶点的三角形是直角三角形。
解析试题分析:(1)由∵抛物线 的对称轴是直线x=
的对称轴是直线x= 和经过点A(—1,0),得
和经过点A(—1,0),得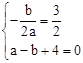 ,解之即可得抛物线的解析式。
,解之即可得抛物线的解析式。
∵抛物线 的对称轴是直线x=
的对称轴是直线x= ,∴
,∴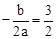 ①。
①。
又∵抛物线 经过点A(—1,0),∴
经过点A(—1,0),∴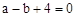 ②。
②。
联立①②,解得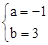 。
。
∴抛物线的解析式为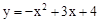 。
。
(2)根据相似三角形和等高三角形的性质,可得 和
和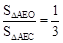 ,从而
,从而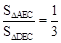 ,即S1:S2=
,即S1:S2= 。
。
在 中令x=0得
中令x=0得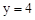 ,∴C(0,4)。
,∴C(0,4)。
∵抛物线 的对称轴是直线x=
的对称轴是直线x= ,CD//x轴交抛物线于点D,∴D(3,4)。
,CD//x轴交抛物线于点D,∴D(3,4)。
又OA=1,CD=3,
∵CD//x轴,∴△AEO∽△DEC。∴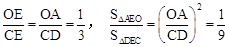 ③。
③。
又∵△AEO和△AEC是两等高三角形,∴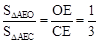 ④。
④。
③÷④,得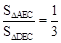 ,即S1:S2=
,即S1:S2= 。
。
(3)分四种情况讨论:
①当点P在EC上运动,∠PDQ=900时,如图1,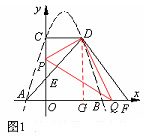
过点D作DG⊥AB于G,则CD=3,PC= 3—3t,GD=4,QG=3—2t,
由△PCD∽△QGD得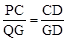 ,即
,即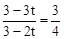 ,解得
,解得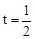 。
。
②当点P在CD上运动,∠PDQ=900时,如图2,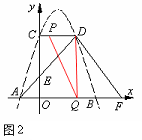
OQ=6—2t,CD=3,此时,OQDC是矩形。由OQ=CD,即6—2t=3解得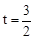 。
。
③当点P在CD上运动,∠QPD=900时,如图3,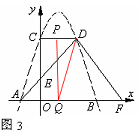
OQ=6—2t,CP=3t—3,此时,OQPC是矩形。由OQ=CP,6—2t=3t—3解得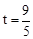 。
。
④当点P在DF上运动,∠QPD=900时,如图4,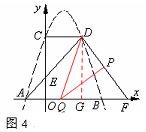
由D(3,4),F(6,0),根据勾股定理可得DF=5。
过点D作DG⊥AB于G,则DF=5,GF=3, PF= 11—3t, QF=2t,
由△FPQ∽△FGD得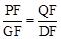 ,即
,即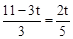 ,解得
,解得 。
。
综上所述,当 时,以D、P、Q为顶点的三角形是直角三角形。
时,以D、P、Q为顶点的三角形是直角三角形。


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
(本小题满分12分)如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(1)b= ,点B的横坐标为 (上述结果均用含c的代数式表示);
(2)连接BC,过点A作直线AE∥BC,与抛物线 交于点E.点D是x轴上一点,其坐标为
交于点E.点D是x轴上一点,其坐标为
(2,0),当C,D,E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连接PB,PC,设所得△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的△PBC共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线抛物线 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
①若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得得线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价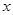 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图.在平面直角坐标系中,边长为 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.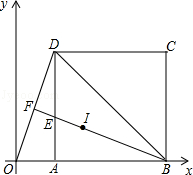
(1)求证:△OAD≌△EAB;
(2)求过点O、E、B的抛物线所表示的二次函数解析式;
(3)在(2)中的抛物线上是否存在点P,其关于直线BF的对称点在x轴上?若有,求出点P的坐标;
(4)连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数 (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.
(1)写出A、B两点的坐标(坐标用m表示);
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式;
(3)设以AB为直径的⊙M与y轴交于C、D两点,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知点A(0,4),B(2,0).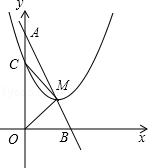
(1)求直线AB的函数解析式;
(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x﹣m)2+n与线段OA交于点C.
①求线段AC的长;(用含m的式子表示)
②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com