
如图,△ABC的面积为1.分别倍长(延长一倍)AB,BC,CA得到△A1B1C1.再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长n次后得到的△AnBnCn的面积为 .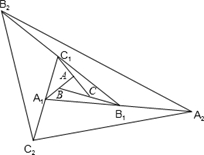

解析试题分析:先根据图形特征找出延长各边后得到的三角形的面积是原三角形的面积的倍数的规律,再利用发现的规律求延长第n次后的面积.
△AA1C=3△ABC=3,
△AA1C1=2△AA1C=6,
所以△A1B1C1=6×3+1=19;
同理得△A2B2C2=19×19=361;
△A3B3C3=361×19=6859,
△A4B4C4=6859×19=130321,
△A5B5C5=130321×19=2476099,
从中可以得出一个规律,延长各边后得到的三角形是原三角形的19倍,所以延长第n次后,得到△AnBnCn,
则其面积为 .
.
考点:找规律-图形的变化
点评:解题的关键是仔细分析所给图形的特征得到规律,再把这个规律应用于解题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
 如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是
如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为| 3 |
| 4 |
| 3 |
| 42 |
| 3 |
| 43 |
| 3 |
| 4n |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC的面积为
如图,△ABC的面积为| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连结A2,B2,C2,得到△A2B2C2.…按此规律,要使得到的三角形的面积超过2013,最少经过查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com