
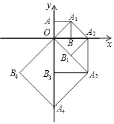
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依次规律,则点A8的坐标是_____.
【答案】(0,16)
【解析】
根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以![]() ,所以可求出从A到A3的后变化的坐标,再求出A1、A2、A3、A4、A5,得出A8即可.
,所以可求出从A到A3的后变化的坐标,再求出A1、A2、A3、A4、A5,得出A8即可.
根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以![]() ,
,
∵从A到A3经过了3次变化,
∵45°×3=135°,1×(![]() )3=2
)3=2![]() ,
,
∴点A3所在的正方形的边长为2![]() ,点A3位置在第四象限,
,点A3位置在第四象限,
∴点A3的坐标是(2,﹣2),
可得出:A1点坐标为(1,1),
A2点坐标为(2,0),
A3点坐标为(2,﹣2),
A4点坐标为(0,﹣4),
A5点坐标为(﹣4,﹣4),
A6点坐标为(﹣8,0),
A7点坐标为(﹣8,8),
A8点坐标为(0,16),
故答案为(0,16).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知PA、PB切⊙O于A、B两点,CD切⊙O于E,△PCD的周长为20,sin∠APB=![]() ,则⊙O的半径( )
,则⊙O的半径( )
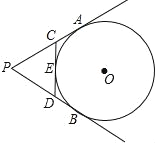
A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是我市全面推进中小学校“社会主义核心价值观”教育年.某校对全校学生进行了中期检测评价,检测结果分为![]() (优秀)、
(优秀)、![]() (良好)、
(良好)、![]() (合格)、
(合格)、![]() (不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表(图1)和统计图(图2).
(不合格)四个等级.并随机抽取若干名学生的检测结果作为样本进行数据处理,制作了如下所示不完整的统计表(图1)和统计图(图2).
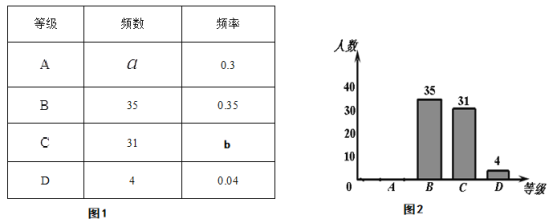
请根据图1、图2提供的信息,解答下列问题:
(1)本次随机抽取的样本容量为
(2)![]() ,
,![]() .
.
(3)请在图2中补全条形统计图.
(4)若该校共有学生800人,据此估算,该校学生在本次检测中达到“![]() (优秀)”等级的学生人数为 人.
(优秀)”等级的学生人数为 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
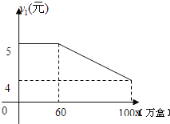
【题目】有一个茶叶厂,该厂的茶叶主要有两种销售方式,一种方式是卖给茶叶经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的茶叶都可以全部销售,该茶叶厂每年可以生产茶叶100万盒,其中,卖给茶叶经销商每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数关系如图15所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:当0≤x<40时, y2=—0.75x+80,
当40≤x≤100时 y2=40.
(1)写出该茶叶厂卖给茶叶经销商的销售总利润z1(万元)与其销售量x(万盒)之间的函数关系式,并指出x的取值范围;
(2)写出该茶叶厂在各超市柜台销售的总利润z2(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式及x取值范围;
(3)求该茶叶厂每年的总利润w(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式,并帮助该茶叶厂确定卖给茶叶经销商和在各超市柜台的销量各为多少万盒时,该公司的年利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某品牌的一款学生斜持包,其挎带由单层部分、双层部分和调节扣组成.设单层部分的长度为xcm,双层部分的长度为ycm,经测景,得到如下数据:
x(cm) | 0 | 4 | 6 | 8 | 10 | … | 120 |
y(cm) | M | 58 | 57 | 56 | 55 | … | n |
(1)如图2,在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用平滑曲线连接,并根据图象猜想求出该函数的解析式;
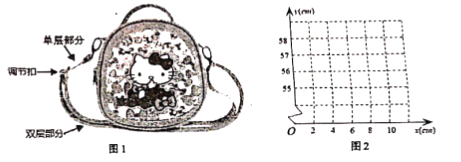
(2)若小花要购买一个持带长为125cm的斜挎包,该款式的斜挎包是否满足小花的需求?请说明理由,(挎带的总长度=单层部分长度+双层部分长度,其中调节扣的长度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
对于线段的垂直平分线我们有如下结论:到线段两个端点距离相等的点在线段的垂直平分线上.即如图①,若PA=PB,则点P在线段AB的垂直平分线上.

请根据阅读材料,解决下列问题:
如图②,直线CD是等边△ABC的对称轴,点D在AB上,点E是线段CD上的一动点(点E不与点C、D重合),连结AE、BE,△ABE经顺时针旋转后与△BCF重合.
(1)旋转中心是点 ,旋转了 (度);
(2)当点E从点D向点C移动时,连结AF,设AF与CD交于点P,在图②中将图形补全,并探究∠APC的大小是否保持不变?若不变,请求出∠APC的度数;若改变,请说出变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
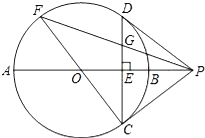
【题目】如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
(1)判断直线PD与⊙O的位置关系,并加以证明;
(2)联结CO并延长交⊙O于点F,联结FP交CD于点G,如果CF=10,cos∠APC=![]() ,求EG的长.
,求EG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com