
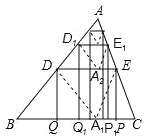
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
【答案】B
【解析】
试题分析:连接AA1,
由折叠的性质可得:AA1⊥DE,DA=DA1,
又∵D是AB中点,
∴DA=DB,
∴DB=DA1,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE∥BC,
∴AA1⊥BC,
∴四边形DEPQ的面积为S1=DQ×DE=(AA1﹣AA2)×DE=(1﹣![]() )AA1×
)AA1×![]() BC=(1﹣
BC=(1﹣![]() )×
)×![]() ×2S△ABC=(1﹣
×2S△ABC=(1﹣![]() )×
)×![]() ×2
×2
同理,四边形D1E1P1Q1的面积为S2=D1Q1×D1E1=(AA1﹣AA3)×D1E1=(1﹣![]() )×
)×![]() ×2
×2
四边形D2E2P2Q2的面积为S3=D2Q2×D2E2=(AA1﹣AA4)×D2E2=(1﹣![]() )×
)×![]() ×2
×2
…
∴Sn的值为:[1﹣(![]() )n]×(
)n]×(![]() )n×2=
)n×2=![]()
故选(B)


科目:初中数学 来源: 题型:
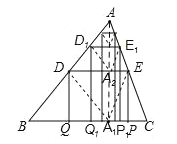
【题目】如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
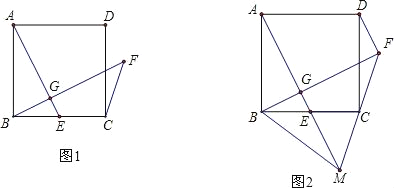
(1)求证:AG=FG;
(2)如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若|a|=-a,|b|=b,|c|=-c,|d|=-d,a,b,c,d都不为零,并且|a|>|b|>|c|>|d|,请把a,b,c,d四个数从小到大用“<”号连结.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个多项式与3x2+9x的和等于3x2+4x-1,则这个多项式是( )
A. -5x-1 B. 5x+1 C. -13x-1 D. 13x+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面等式成立的是( )
A. 83.5°=83°50′ B. 37°12′36″=37.48°
C. 24°24′24″=24.44° D. 41.25°=41°15′
查看答案和解析>>
科目:初中数学 来源: 题型:
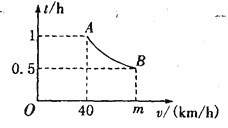
【题目】一辆汽车匀速通过某段公路,所需时间![]() 与行驶速度
与行驶速度![]() (km/h)满足函数表达式
(km/h)满足函数表达式![]() .其图像为如图所示的一段曲线,且端点为A(40,1)和B(
.其图像为如图所示的一段曲线,且端点为A(40,1)和B(![]() ,0.5)
,0.5)
(1)求k和m的值。
(2)若行驶速度不能超过60 km/h,则汽车通过该路段最少需要多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com