
分析 将方程的解代入方程得到m-2n=2,m2-4mn+4n2可分解为(m-2n)2,然后代入计算即可;
依据多项式乘多项式法则可得到ax2+bx+c=(x-1)(x-2)=x2-3x+2,然后可得到a、b、c的值.
解答 解:将$\left\{\begin{array}{l}x=1\\ y=-2\end{array}\right.$代入mx+ny=2得:m-2n=2,
∵m2-4mn+4n2=(m-2n)2,
∴原式=22=4.
∵ax2+bx+c=(x-1)(x-2)=x2-3x+2,
∴a=1,b=-3,c=2,
∴a+b+c=1-3+2=0.
故答案为:4;0.
点评 本题主要考查的是因式、二元一次方程的解的定义,熟练掌握完全平方公式、多项式乘多项式法则是解题的关键.


科目:初中数学 来源: 题型:选择题
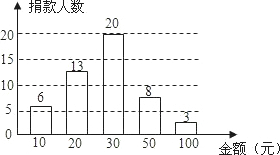 某校九年级(1)班50名学生积极参加献爱心慈善捐款活动,班长将捐款情况进行统计,并绘制成了如图所示的统计图,根据统计图提供的信息,捐款金额中位数是( )
某校九年级(1)班50名学生积极参加献爱心慈善捐款活动,班长将捐款情况进行统计,并绘制成了如图所示的统计图,根据统计图提供的信息,捐款金额中位数是( )| A. | 25 | B. | 50 | C. | 35 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
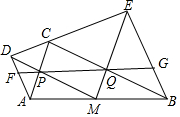 如图,在Rt△ABC中,∠ACB=90°,分别以AC、AB为斜边向△ABC外作等腰直角△ACD和等腰直角△BCE,取AB的中点M,连接MD,ME分别交AC、BC于点P、Q,直线PQ分别交AD、BE于点F、G.有以下结论:①△MDE是等腰直角三角形;②PQ=PF+QG;③△APF∽△EQG;④S△ACD+S△BCE=S△ABC.
如图,在Rt△ABC中,∠ACB=90°,分别以AC、AB为斜边向△ABC外作等腰直角△ACD和等腰直角△BCE,取AB的中点M,连接MD,ME分别交AC、BC于点P、Q,直线PQ分别交AD、BE于点F、G.有以下结论:①△MDE是等腰直角三角形;②PQ=PF+QG;③△APF∽△EQG;④S△ACD+S△BCE=S△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
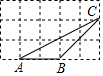 如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )
如图,△ABC的顶点都在方格纸(每个小正方形的边长均为1)的格点上.则tan∠A=( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com