练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知：四边形ABCD如图所示．
    （1）填空∠A+∠B+∠C+∠D=360°
    （2）请用两种方法证明你的结论．

    分析 （1）利用四边形的内角和为360°直接回答即可；
    （2）转化为三角形的内角和定理求解即可．

    解答 解：（1）∠A+∠B+∠C+∠D=360°，
    故答案为：360°．
    （2）方法一：
    连接AC，把四边形分成两个三角形，
    一个三角形内角和为180°，所以两个三角形的内角和为360°，
    四边形的内角和是360．
    方法二：
    ∵三角形内角和为180°，
    ∴4个三角形的内角和为4×180°=720°，
    ∴四边形内角和为：720°-∠1-∠2-∠3-∠4=720°-360°=360°．

    点评 本题考查了多边形的内角和外角，三角形的内角和外角的知识，解题的关键是能够将多边形转化为三角形来求解，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

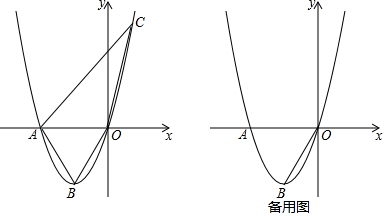
    13．将Rt△AOB 如图放置在直角坐标系中，并绕O点顺时针旋转90°至△COD的位置，已知A（-2，0），∠ABO=30°．则△AOB旋转过程中所扫过的图形的面积为（　　）
    A．$\frac{11π}{3}+2\sqrt{3}$B．$3π+2\sqrt{3}$C．$3π+\sqrt{3}$D．$\frac{11π}{3}+\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，⊙O的直径AB=10，弦AC=6，∠BAC的平分线交⊙O于点D，过点D作⊙O的切线交AC的延长线于点E．求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在平面直角坐标系中，正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象经过点（2，2）．
    （1）分别求这两个函数的表达式；
    （2）将直线OA向上平移3个单位长度后与y轴交于B，与反比例函数图象在第一象限内的交点为C，连接AB，AC，求点C的坐标及△ABC的面积；
    （3）反比例函数图象上是否存在点D，使DC⊥BC？若存在，请求出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．每年4月23日为“世界读书日”，某校开展了“好书伴我成长”的读书征文活动，该校九年级共有375人，征文活动设一等奖五人，二等奖二十人，三等奖五十人．
    （1）请直接写出该年级学生获奖的概率；
    （2）若获得一等奖的五名同学中，有三名女生，两名男生，准备在获得一等奖的五名同学中任选两人做汇报交流，请计算恰好选出一名男生和一名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

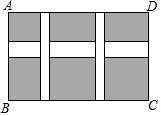    8．如图，某小区规划在一个长40米，宽36米的矩形场地ABCD上修建横、纵道路宽为3：2的三条道路，使其中两条与AB平行，另一条与AD平行，其余部分种草，若使每一块草坪的面积都为198平方米，求道路的宽度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在平面直角坐标系中，点A的坐标为（-2，0），将线段OA绕原点O逆时针旋转60°，得到线段OB，抛物线y=ax2+bx+c经过A、O、B三点．
    （1）求此抛物线的解析式；
    （2）点C是x轴上方的抛物线上的一点，且四边形ABOC被x轴分成面积比为1：2的两部分，求点C的坐标；
    （3）若点D是y轴正半轴上的动点，经过D点与x轴平行的直线l与抛物线交于M、N两点（M点在N点右侧），是否存在这样的D点，使得以MN为直径的圆恰好经过原点O？若存在，求出D点坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

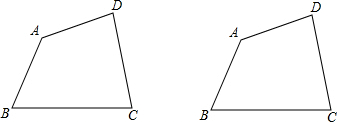
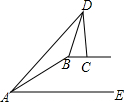    12．如图，在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面，小明在斜坡底A处测得该纪念碑顶部D的仰角为45°，然后他沿着坡比i=5：12的斜坡AB攀行了39米到达坡顶，在坡顶B处又测得该纪念碑顶部的仰角为68°．求坡顶B到地面AE的距离和纪念碑CD的高度．（结果精确到1米，参考数据：sin68°=0.9，cos68°=0.4，tan68°=2.5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，平行四边形ABCD内接于⊙O，则∠ADC=（　　）
    A．45°B．50°C．60°D．75°

    查看答案和解析>>

    同步练习册答案