
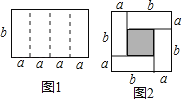
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=5,xy=4,求x﹣y的值.
【答案】(1)(b﹣a)2;(2)(a+b)2﹣(a﹣b)2=4ab;(3)x﹣y=±3.
【解析】
(1)阴影部分为边长为(b-a)的正方形,然后根据正方形的面积公式求解;
(2)在图2中,大正方形有小正方形和4个矩形组成,则![]()
(3)由(2)的结论得到(x+y)2-(x-y)2=4xy,再把x+y=5,xy=4代入得到(x-y)2=9,然后利用平方根的定义求解.
(1)阴影部分为边长为(b﹣a)的正方形,所以阴影部分的面积(b﹣a)2;
(2)图2中,用边长为a+b的正方形的面积减去边长为b﹣a的正方形等于4个长宽分别a、b的矩形面积,
所以![]()
(3)由(2)得![]()
把x+y=5,xy=4代入得![]()
则xy=±3.


科目:初中数学 来源: 题型:
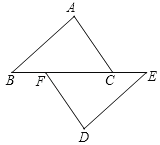
【题目】如图,点B、F、C、E在同一条直线上,点A、D在直线BC的异侧,AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)若∠BFD=150°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC. 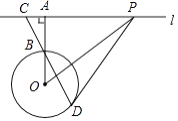
(1)求证:PD是⊙O的切线;
(2)若AC=1,AB=2,PD=6,求⊙O的半径r和△PCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
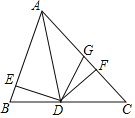
【题目】如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y= ![]() x+4,与x轴相交于点D.
x+4,与x轴相交于点D.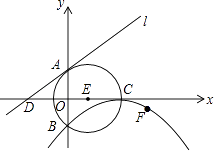
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3)动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,那么关于此二次函数的下列四个结论: ①a<0;②c>0;③b2﹣4ac>0;④ ![]() <0中,正确的结论有( )
<0中,正确的结论有( )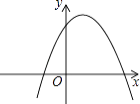
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列例题
解方程:|x|+|2x﹣1|=5.
解:①当x≥0.5时,原方程可化为:x+2x﹣1=5,它的解是x=2;
②当0≤x<0.5时,原方程可化为:x﹣2x+1=5,解之,得x=﹣4,
经检验x不合题意,舍去.
③当x<0时,原方程可化为:﹣x﹣2x+1=5,它的解是x=﹣![]() .
.
所以原方程的解是x=2或x=﹣![]() .
.
(1)根据上面的解题过程,写出方程2|x﹣1|﹣x=4的解.
(2)根据上面的解题过程,解方程:2|x﹣1|﹣|x|=4.
(3)方程|x|﹣2|x﹣1|=4是否有解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com